Funktion auf Stetigkeit und Differenzierbarkeit untersuchen? f(x)=x^5 und f(x)= 5. Wurzel aus x

Question

Ich soll die folgenden Funktionen auf Stetigkeit und Differenzierbarkeit untersuchen:

f(x)=x⁵

f(x)=⁵√x

Wie genau wird sowas gemacht? Ich kenne das bisher nur mit der Angabe konkreter Punkte.

Danke euch! :)

Comments

Ich nehme an, dass ihr links- und rechtsseitige Grenzwerte verglichen habt, wenn du da Punkte untersucht hast.

Wenn du keine Definitionslücken, Pole, Knickstellen… betrachtest, kannst du das in der Regel global erledigen. Grundrechenarten + - * führen zu keinen Schwierigkeiten bei Differenziebarkeit und Stetigkeit.

 

f(x)=x⁵

Definitionsbereich R. Wertebereich R. y=x ist stetig. x*x , x*x*x und x^5 auch.

f(x)=⁵√x

Definitions- und Wertebereich für Wurzelfunktionen üblicherweise R+_o 

Einzige fragliche Stelle: x=0. Die Funktion ist rot zwar stetig aber nicht differenzierbar. Da ihre Umkehrfunktion in x=0 eine horizontale Tangente hat, hat ^5 √x in x = 0 eine vertikale Tangente. Steigung nicht definiert in R (müsste ± unendlich sein)

Fortsetzung in meiner Antwort unten.

Answer 1

"Ich soll hier die Stetigkeit von der Funktion f(x) = fünfte Wurzel von x = x^1/5 auf Stetigkeit überprüfen, aber als Definitionsbereich ist f:R->R angegeben. Die ist doch aber nur für f:[0,R+) definiert, oder?"

Zitat: Präzision aus dem eben geschlossenen Duplikat.

Da y=x^5 jedem Element aus R eindeutig ein Element aus R zuordnet, kann man ohne Probleme eine Umkehrung auf ganz R machen und die 5. Wurzel aus negativen Zahlen auch definieren.

Das geht nur bei ungeraden Wurzeln und ist nicht wirklich üblich. (Bei geraden Wurzeln muss man immer den Definitionsbereich auf einen Ast der Potenzfunktion, die umgekehrt wird, einschränken)

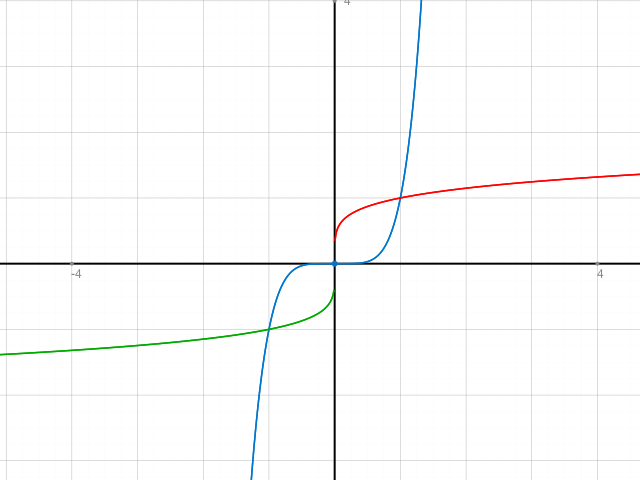
Illustration: Werden die beiden Äste von y=x^5 an y=x gespiegelt, erhält man die Kombination aus rot und grün.

Hier wird keinem Element jedem Element von R genau eine 5. Wurzel zugeordnet. Deshalb handelt es sich um eine Funktion.