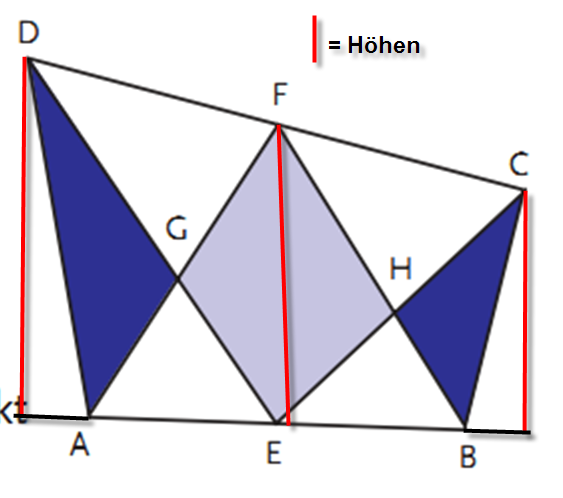
Da die Höhen (siehe Bild) parallel sind, kann man den Strahlensatz auf sie anwenden. Da der Punkt F die Strecke CD in zwei gleich grosse Teile teilt, gilt: Die Höhe des Dreiecks ABF ist gleich dem Mittelwert der Höhe des Dreiecks ADE und BCE.
Gemäss Behauptung gilt: Fläche AGD + Fläche BCH = Fläche EHFG
Dann gilt auch: Fläche ADE + Fläche BCE = Fläche ABF (weil die kleinen Dreiecke AEG und EBH gemeinsame Flächen des Vierecks und der beiden Dreiecke sind)
Die Dreiecks-Fläche ist gleich Grundseite * Höhe / 2. Also gilt:
Fläche ADE = h_1 * AE / 2
Fläche BCE = h_3* EB / 2
Fläche ABF = h_2 * (AE + EB) / 2
h_2 = (h_1 + h_3) / 2 (arithm. Mittel)
Daraus folgt:
h_1 * AE / 2 + h_3* EB / 2 = h_1 * AE / 2 + h_3* AE / 2 = (h_1 + h_3) / 2* AE
h_2 * (AE + EB) / 2 = (h_1 + h_3) / 2 * (AE + EB) / 2 = (h_1 + h_3) / 2 * (2 * AE) / 2 = (h_1 + h_3) / 2 * AE
Wenn man die kleinen Dreiecke wieder abzieht, erhält man Fläche AGD + Fläche BCH = Fläche EHFG