Berechne die Länge der Strecke x

Question

Berechnung der Strecke x am Dreieck

Comments

bearbeitetes Bild (falls es sich tatsächlich um ein rechtwinkliges Dreieck handlen sollte):

Answer 1

mein Versuch, ganz ohne Pythagoras:

 

Comments

Wenn das Dreieck rechtwinklig ist gilt:

x/12 = 15/√(36^2 - 15^2) --> x = 60/119·√119 ≈ 5.5002

Das würde sich mit Pythagoras anstatt mit der Trigonometrie exakt berechnen lassen.

Wenn das Dreieck nicht rechtwinklig ist, dann wäre die Aufgabe nicht lösbar, weshalb ich auch davon ausgehen würde, dass es rechtwinklig sein soll.

Answer 2

Die Verlängerung der 12 m soll z genannt werden. Dann lässt sich z mit Pythagoras bestimmen (12+z)²+15²=36² Das Ergebnis für z ist irrational. Damit weigere ich mich, weiter zu rechnen.

Comments

So ganz irrational sieht die Länge in der
Skizze aber nicht aus. Siehe meine Berechnung.

---

Wie sieht denn eine irrationale Länge im Vergleich zu einer nicht irrationalen Länge aus?

---

Ich nehme meinen Kommentar zurück.

Das Ergebnis für z ist irrational
Damit weigere ich mich, weiter zu rechnen.

ich hatte verstanden " imaginär ".
Mit irrationalen Zahlen kann man ja die Aufgabe
zu Ende rechnen.

Answer 3

Untere Streckenlänge berechnen

36^2 = 15^2 + l^2
l = 32.73

15 / 32.73 = x / 12
x = 5.45

Comments

alles reine Spekulation

---

Sollte das äußere Dreieck nicht rechtwinklig sein
ist eine Berechnung nicht möglich.
Es stellt sich dann die Frage nach dem Sinn der Aufgabe_.

---

Es gibt nicht den geringsten Anlass anzunehmen, es könne sich um ein rechtwinkliges Dreieck handeln. (Es sieht noch nicht einmal annähernd rechtwinklig aus.)

Mein Kommentar hat genau auf diesen Sachverhalt hingewiesen.

Der Sinn der Aufgabe besteht darin, dass ihr vor dem blinden Losrechnen erst einmal hättet überprüfen sollen, ob die Voraussetzungen für die Anwendung mathematischer Sätze überhaupt vorliegen.

---

x und 15 sehen in dieser Fotographie tatsächlich nicht parallel aus.

Man müsste den vollständigen Text und den Kontext dieser Aufgabe kennen.

---

Hallo Lu,

die Einstellung der kompletten Fragen zu den Aufgaben würde sicherlich
weiterbringen. Vielleicht heißt es ja " welche der Aufgaben ist lösbar ".

Allzuviel will ich aber nicht spekulieren. Das lohnt nicht.

Answer 4

Planfigur:

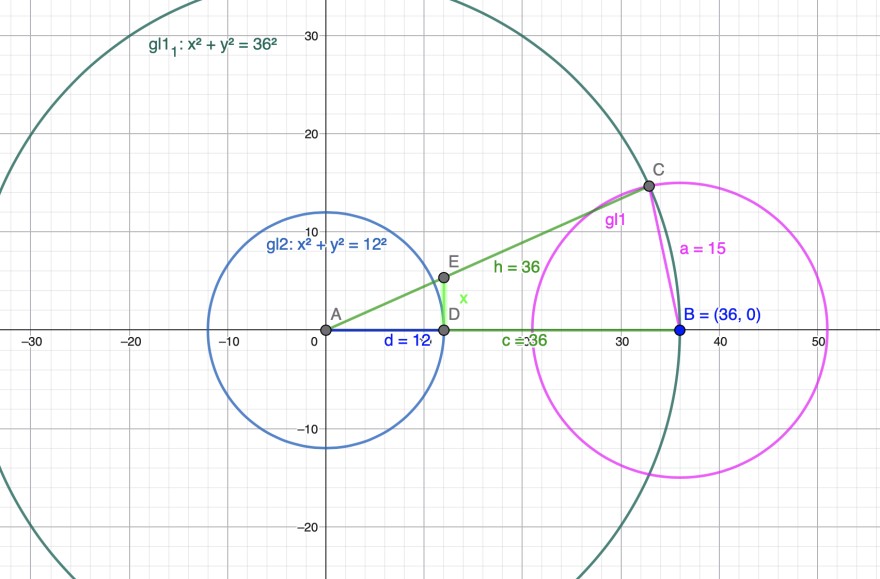
Kreis um Ursprung mit  \( r=12 \) :    \( x^2+y^2=144 \)  schneidet die x-Achse in D\( (12|0) \)

Kreis um Ursprung mit \( r=36  \) :   \( x^2+y^2=1296 \) schneidet die x-Achse in B\( (36|0) \)

Kreis um B\( (36|0) \) mit  \( r=15 \): \( (x-36)^2+y^2=225 \)

schneidet   \( x^2+y^2=144 \) Kreis um Ursprung mit \( r=36  \):

\( x^2+y^2-1296=(x-36)^2+y^2-225 \)   →   \( x=\frac{263}{8}\) und \( y≈14,67\)

Gerade durch A und E:   \( y≈0,45x\).

Die Senkrechte in D(12|0) ist \( x=12 \) . Sie schneidet \( y≈0,45x\)    in E(12|5,4)

Somit ist die gesuchte Länge ungefähr 5,4m lang.

Comments

ungefähr 5,4m lang

Es sind eher 5,5 und das ziemlich genau.

Das steht aber auch erst seit bald 10 Jahren in meiner Antwort auf dieser Seite.

---

Du bist von 2 rechten Winkeln ausgegangen. Das ist aber vom FS schon angemahnt worden.

---

Und du gehst davon aus, dass die Grundseite des großen Dreiecks ebenso 36 m lang ist und es sich damit um ein gleichschenkliges Dreieck handelt?

Jetzt schau dir mal die originale Skizze an.

---

Leute, er möchte doch einfach nur seinen Senf loswerden und einen anderen - künstlich aufgeblähten - Ansatz zeigen. Dass er dabei ständig die Aufgabenstellung missachtet, ist doch nichts Neues.

---

Hier ist ein neuer Ansatz: Dann gibt es aber auch mehrere Längen von x

@Apfelmännchen Lass doch mal diese beleidigenden Kommentare!

---

Ich sehe da keine Beleidigung, sondern Fakten: deine Antworten sind häufig künstlich aufgebläht und die Aufgabenstellung ignorierst du auch oft, nur um einen alternativen Ansatz zu liefern. Wenn du dich vom Senf beleidigt fühlst, tut mir das allerdings sehr leid für dich.

Und davon abgesehen: Du lässt Deine überflüssigen Antworten doch auch nicht, obwohl das von mehreren kritisiert wird. Bevor Du also irgendwelche Forderungen stellst, fang bei dir selbst an. Danke.