Steckbriefaufgabe. Funktionsgleichung der ganzrationalen Funktion dritten Grades mit T(1|-1) und H(-1|3)?

Question

bestimmen Sie die zugehörige Funktionsgleichug.

Der Graph einer ganzrationalen Funktion dritten Grades hat in T(1|-1) einen Tiefpunkt und in H(-1|3) einen Hochpunkt.

Brauch bitte Hilfe bei der Aufgabe. Es wäre gut wenn jemand das vorrechnen könnte und jeden einzelnen Schritt auch aufschreibt.

Danke !!!

Answer 1

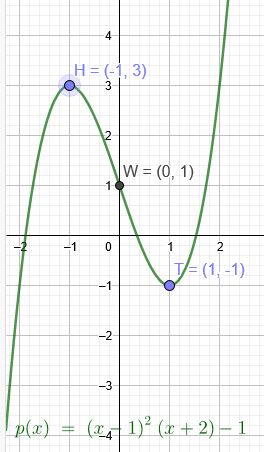
Der Graph einer ganzrationalen Funktion dritten Grades hat in $T(1|-1)$ einen Tiefpunkt und in $H(-1|3)$ einen Hochpunkt.

Durch die Lage des Tief-und Hochpunktes liegt der Wendepunkt bei $W(0|1)$

Ich verschiebe den Graphen um eine Einheit nach oben

$T(1|-1)$→$T´(1|0)$  Hier ist nun eine doppelte Nullstelle.

$H(-1|3)$→$H´(-1|4)$

$W(0|1)$→$W´(0|2)$

$f(x)=a•(x-1)^2(x-N)$

$f(-1)=4a•(-1-N)$  

$4a•(-1-N)=4$  → $a=\frac{1}{-1-N}$→ $a=-\frac{1}{1+N}$

$f(x)=-\frac{1}{1+N}•(x-1)^2(x-N)$

$f(0)=\frac{1}{1+N}•N$

$\frac{1}{1+N}•N=2$     $N=-2$   $a=1$

$f(x)=(x-1)^2(x+2)$

Nun eine Einheit nach unten:

$p(x)=(x-1)^2(x+2)-1$

Answer 2

Der Graph einer ganzrationalen Funktion dritten Grades hat in T(1|-1) einen Tiefpunkt und in H(-1|3) einen Hochpunkt.

Ansatz f(x)=ax³+bx² +cx+d. T(1|-1)  und H(-1|3) einsetzen. Das ergibt zwei Gleichungen. Ableitung f '(x)=3ax² +2bx+c. Sowohl f '(1) =0 als auch f '(-1)=0. Also 0 = 3a+2b+c und 0=3a-2b+c. Jetzt dasSystem von vier Gleichungen mit vier Unbekannten lösen-

Answer 3

Der Graph einer ganzrationalen Funktion dritten Grades hat in T(1|-1) einen Tiefpunkt und in H(-1|3) einen Hochpunkt.

f(x) = ax³ +bx² + cx + d

f(1) = -1

f ' (1) = 0

f( -1) = 3

f ' (-1) = 0

mit f ' (x) =  3a x² + 2bx  + c   und f(x) = ax³ +bx² + cx + d

ein Gl.syst. bilden und abcd ausrechnen.

Gibt f(x) = x³ - 3x + 1