Wie löse ich nach r auf?

Question

131=130(1+r)-0,6(1+r)^0,5-13(1+r)^1/6

Löse nach r auf

Answer 1

Mir fällt keine analytische Lösung ein. Ich denke dass mus man numerisch (Newton-Verfahren) lösen.

Answer 2

statt r nehme ich das übliche x:

131=130*(1+x)-6/10*(1+x)^1/2-13*(1+x)^1/6

Dazu gibt es leider keine Umkehrfunktion -> also auch keine explizite Umstellung! Man kann noch

650 x - 3 sqrt(x + 1) - 65 (x + 1)^1/6 = 5

und dann erweitern zu

75418890625000000 x⁶ - 3485691543750000 x⁵ + 62268575167500 x⁴ - 2628295495229 x³ - 2054048729862 x² - 43446005287 x - 75557297529=0

ABER Polynome sind nur bis Grad 4 explizit lösbar (bis auf wenige Sonderfälle auch höhere Grade).

Bleiben nur Näherungsverfahren, die man aber auch beliebig genau bekommt.

http://www.lamprechts.de/gerd/php/gleichung-6-grades.php

ist dafür wie geschaffen.

Von den 6 möglichen Lösungen ist nur x2 eine echte Lösung der Ausgangsgleichung:

0.114385963289781677714172435118320576471726761342114467168261554...

Wenn es eine Hausaufgabe ist, lautet die Gleichung bestimmt anders, denn Lehrer wollen meist glatte Ergebnisse oder umstellbare Formeln...

Oder hattet Ihr schon das Newton-Verfahren:

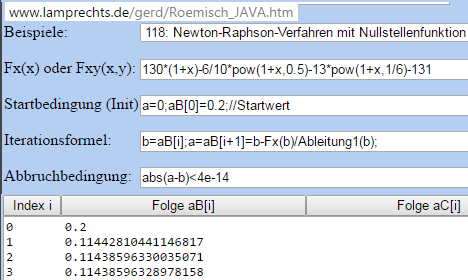
Nach 3 Schritten ist mögliche Genauigkeit für Typ double ausgeschöpft.