Modellieren Brückenboge Höhe

Question

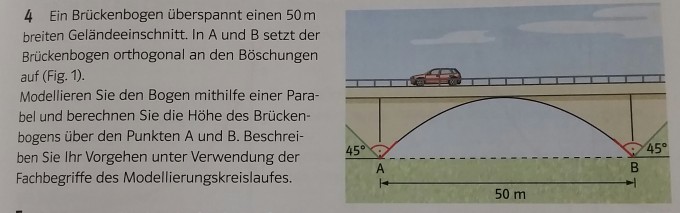
ich habe eine Aufgabe mit Lösung aber ich verstehe die Lösung nicht ganz. Die Aufgabe habe ich als Bild hinzugefügt. Ich weiß, dass man erst die Funktion und die Ableitung bilden muss. Also f (x)=ax^2+bx+c

 und f'(x)=2ax+b. Dann nimmt man ja den Punkt A als A (0/0).

Dann werde ich aber unsicher.

Dann steht als Lage: f (0)=0  a*0^2+b*0+c=0  c=0

Das ist ja eigentlich der Punkt A in die Funktion f (x) eingefügt.

Jetzt kommt man eigentliches Problem

Bei Steigung steht f'(0)=1   2a*0+b=1   b=1

Ich verstehe jetzt nicht woher f'(0)=1 herkommt. Ich habe ja eigentlich nur den Punkt (0/0).  

Ich hoffe ihr könnt mir das erklären woher das kommt.

MFG 

Comments

Damit der Parabelbogen im Ursprung mit Steigungswinkel von 45° beginnen soll, muss die Steigung 1 sein.

Answer 1

" Ich verstehe jetzt nicht woher f'(0)=1 herkommt. Ich habe ja eigentlich nur den Punkt (0/0). "

Du hast zudem noch eine Zeichnung. Links ist 45° angeschrieben.

Dann siehst du einen roten Bogen mit einem Punkt. Das bedeutet 90°.

Folglich ist der Steigungswinkel im Punkt A gerade 45°. Das ergibt die Steigung m=1. 

Also: f '(0) = 1. 

Answer 2

Damit der Parabelbogen im Ursprung mit Steigungswinkel von 45° beginnen soll, muss die Steigung 1 sein.

Allgemeiner Ansatz

f(x) = a·x^2 + b·x + c

f'(x) = 2·a·x + b

Bedingungen und Gleichungen

f(0) = 0 --> c = 0

f'(0) = 1 --> b = 1

f(50) = 0 --> 2500·a + 50·b + c = 0

f'(50) = -1 --> muss aufgrund der Symmetrie eh richtig sein

Wir setzen b und c in die 3. Gleichung ein und lösen nach a auf.

2500·a + 50·1 + 0 = 0 --> a = -0.02

Damit lautet die Funktion

f(x) = -0.02·x^2 + x

Höhe des Brückenbogens

f(25) = -0.02·25^2 + 25 = 12.5 m