ganzrationale Funktion, woher weiss ich, dass es ein globales Minimum ist?

Question

 

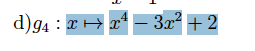
Lösung des Lehrers:

  

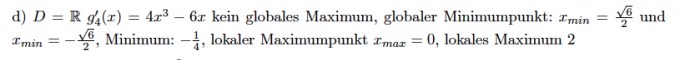
Ich habe die potentiellen Extremstellen berechnet:

Extrempunkt 1 in (0/2) Maximum, da  f'' (0) = -6 < O : Maximum

E2 (√(3/2)/-0.25) Minimum, da f'' (√(3/2)) = 12> O : Mimimum

E3 (-√(3/2)/-0.25) Minimum, da f'' (-√(3/2)) = 12> O : Mimimum

ABER wie kann ich rechnerisch bestimmen / erkennen, dass es sich, so wie in Lösung angegeben um ein globales Minimum bei E2 und E3 handelt?

Wie kann ich rechnerisch bestimmen / erkennen, dass es sich, so wie in Lösung angegeben um kein globales Maximum bei E1 handelt?

Denn schließlich ist D=R.

Vielen Dank für Eure HIlfe!

Comments

Auch hier hilft dir vorerst ein plotter um deine Rechnungen zu kontrollieren.

https://www.matheretter.de/rechner/plotlux

Mit der Zeit kannst sogar du ohne Plotter eine Skizze erstellen. 

Answer 1

weil lim x ---> ±∞ f(x)=∞ und die Funktion stetig ist, daher kann es kein globales Maximum geben. 

Answer 2

E1 ( 0 | 2 )  Krümmung -6 ; Hochpunkt
E2 (  + √ (3/2) | - 1/4 ) Krümmung 12 : Tiefpunkt
E3 (  - √ (3/2) | - 1/4 ) Krümmung 12 : Tiefpunkt

Wäre der Def-Bereich eingeschränkt auf
ein Intervall z.B. [ -6 ; 3 ] könnte ein Randmaximum
bzw. -minimum  vorhanden sein. Eine Überprüfung
des Funktionswert mit f ( -6 )  und der Vergleich
mit den gefunden Maxima/ Minima würde
Klarheit bringen.

So :
lim x −> ±∞ [ x^4 - 3x^2 + 2 ] = + ∞

Folgerungen
E1 ist ein lokaler Hochpunkt
( es gibt noch höhere Funktionswerte )

E2 und E3 sind globale Tiefpunkte.
( es gibt keine tieferen Funktionswerte )

Comments

Vielen Dank, ich habe es nun verstanden:)

---

Gern geschehen.
Dazu ist das Forum da.
Falls du weitere Fragen hast dann wieder einstellen.