Lösen einer Gleichung mit x ^4

Question

Ich weiß leider nicht, wie ich diese Gleichung lösen soll - es funktioniert ja weder pq- Formel noch ausklammern...

x⁴ -2x² -x +1 = 0

Schon einmal vielen Dank für die Hilfe :)

Comments

Zu welchem Stoff (Thema, Bildungseinrichtung, Jahr, Ort) gehört denn die Frage und welche Hilfsmittel (GTR, CAS, TK oder was auch immer) dürfen denn angewendet werden?

PS: Wie lautet eigentlich die ursprüngliche Aufgabe?

Answer 1

x^4 - 2·x^2 - x + 1 = 0

Mit einem Näherungsverfahren wie z.B. dem Newtonverfahren erhält man

x = 1.490216120

Schau mal in deinen Aufzeichnungen ob ihr ein Näherungsverfahren besprochen habt.

Comments

Gibt es nicht zwei reelle Lösungen?

---

Doch. Alle Lösungen sind:

x = -1.007552359 - 0.5131157955·i ∨

x = -1.007552359 + 0.5131157955·i ∨

x = 0.5248885986 ∨

x = 1.49021612

Answer 2

Hallo lala,

x⁴ - 2x² - x + 1 = 0

Da die Gleichung keine ganzzahlige Lösung hat (müsste ein Teiler von 1 sein!) , die man durch Probieren finden und dann die Gleichung mit Polynomdivision vereinfachen könnte, bleiben nur 

die Cardano-Formeln (lästig und nur auf Polynomgleichungen anwendbar. Sie liefern dort aber alle Lösungen, also auch die komplexen Nullstellen)

Infos:

http://www.mathe.tu-freiberg.de/~hebisch/cafe/viertergrad.pdf

 oder (auch auf Gleichungen anderer Art anwendbar) ein Näherungsverfahren, z. B. das

Newtonverfahren:

Infos dazu findest du hier:

https://de.wikipedia.org/wiki/Newton-Verfahren

Ausgehend von einem (möglichst guten) Startwert, den man z.B.  zwischen zwei x-Werten  findet, deren Funktionswerte verschiedenes Vorzeichen haben, ergeben sich - wenn das Verfahren konvergiert (vgl. unten #) - immer bessere Werte mit der Formel

x_neu =  x_alt - f(x_alt) / f ' (x_alt)

Hier ergeben  z.B. Startwerte x ≥ 1,2    (hat mein Rechner einfach ausprobiert) 

x	f(x) ≈	f '(x) ≈
2	7	23
1,695652174	1,820858988	11,718994
1,540275442	0,343339272	7,455794496
1,494225451	0,025347748	6,367784816
1,490244828	0,000180201	6,277340276
1,490216122	9,33241E-09	6,276690087
1,49021612	0	6,276690054

und Startwerte  10^-10 < x < 1 - 10^-10   (hat mein Rechner auch einfach ausprobiert)

x	f(x) ≈	f '(x) ≈
0,9	-0,8639	-1,684
0,386995249	0,335903756	-2,316147123
0,532022201	-0,018001489	-2,525738328
0,524894982	-1,60941E-05	-2,521114706
0,524888599	-1,4138E-11	-2,521110276

#
bei  x = -1 , x = 0 und x = 1  konvergiert das Verfahren z.B. nicht.  

Das Problem mit den Startwerten ist meist weniger gravierend und erklärt sich hier vor allem dadurch, dass Nullstellen und Extremstellen in einem kleinen Bereich zusammenliegen:

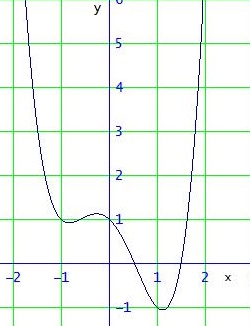
Leider sagt einem das Verfahren auch nicht, wann man alle reellen Nullstellen gefunden hat. Dabei kann einem oft das Betrachten der Ableitungen helfen.

Gruß Wolfgang