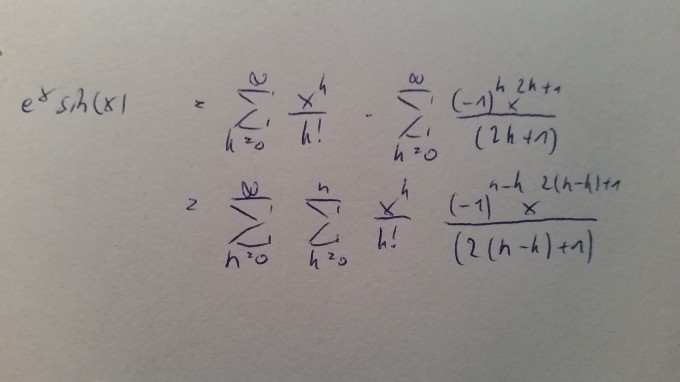Taylorreihe von f(x) = e^{x}*sin(x) mit dessen Cauchy-Produkt

Question

Ich habe folgende Fragestellung:

Berechnen Sie Sie die Taylorreihe von f(x) = e^{x}*sin(x) mit Entwicklungspunkt a = 0 bis zum Koeffizienten von x^4 mit Cauchy-Produkt aus den bekannten Reihen von e^x und sin(x).

Ich bin jetzt so vorgegangen, habe es probiert zusammen zu fassen, aber das klappt irgendwie nicht. Kann mir da bitte jemand helfen?

Comments

Tipp: \(\left(1+x+\tfrac12x^2+\tfrac16x^3+\cdots\right)\cdot\left(x-\tfrac16x^3+\cdots\right)=x+x^2+\tfrac13x^3+0x^4+\cdots\).

Answer 1

Mit dem Tipp von nn (  1/3 x³ kommt ja von 

1*(-1/6) x³ +  1/2 x² * x  ) kommst du doch hin.

Vergleich mit der "normalen " Taylorformel bestätigt die Richtigkeit

f(0) + f ' (0) * x  + f ' ' (0) / 2! * x²  +  f ' ' ' (0) / 3 ! * x³  + f ⁽⁴⁾ (0) * x⁴

= 0    +   1*x    +    2/ 2!  *x²    +    2/ 3!  *x³    +    0/ 4!  *x⁴

=               x       +       x²  +        2/6  *x³    +    0 *x⁴

=               x       +       x²  +        1/3  *x³    +    0          Passt !