Ich brauche Hilfe bei dieser Aufgabe! Bei Aufgabenteil a weiß ich nicht wie ich auf den Grenzwert der Reihe komme. Bei b fehlt mir leider bisher jeglicher Ansatz.
!
(a) Untersuchen Sie die angegebene Folge (an )n∈N im R 3 auf Konvergenz und bestimmen Sie gegebenenfalls ihren Grenzwert.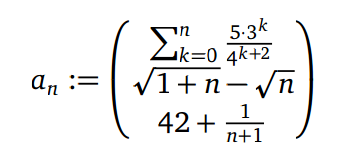
(b) Sei (V, || · ||v) ein vollständiger normierter Raum. Zeigen Sie, dass eine Folge (an )n∈N ⊆ V genau dann konvergiert wenn Sie eine Cauchy-Folge ist.