Ich habe folgende Aufgabe:
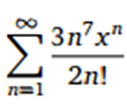
Bestimmen Sie alle x ∈ R mit denen die Potenztreihe konvergiert.
Ich habe dazu folgende Idee:
Zuerst wollte ich schauen ob die Reihe beschränkt ist, da
-> Ist die Folge (n√(an) ) unbeschränkt, so konvergiert die Potenzreihe nur für x = 0.
Dort kam ich dann auf n√(|3n7|) * n√(|1/(2n!)|) * |x|
Das bedeutet doch es gibt eine Schranke mit 3/2*x.
lim(x->∞)( n√(|3n7|)) = ∞ , allerdings ist lim(x->∞)(n√(|1/(2n!)|)) = 0, somit ist lim(x->∞)( n√(|3n7|) * n√(|1/(2n!)|) * |x|) = 0 und ich habe damit eine weiter Schranke.
Somit kann ich den Satz oben nicht anwenden.
Also gilt:
-> Ist ϱ = 0, so konvergiert die Potenzreihe für alle x ∈ K absolut.
Dies bedeutet die Lösung ist, dass die Reihe für alle x konvergiert.
Bin ich richtig vorgegangen?
LG