Berechnung der Lösungen quadratischer Gleichungen und Zerlegung in Linearfaktoren.
a) \(2x^2 - 3x + 1 = 0\)
Ausklammern von 2:
\(2\cdot(x^2 - 1,5x + 0,5)= 0\)
1.Faktor ist \(2\)
Einschub:
Lösungen von \(x^2 - 1,5x + 0,5= 0\) mit den Mitteln deiner Wahl
Ich bekomme:
\(x_1=1\)
\(x_2=0,5\)
.......
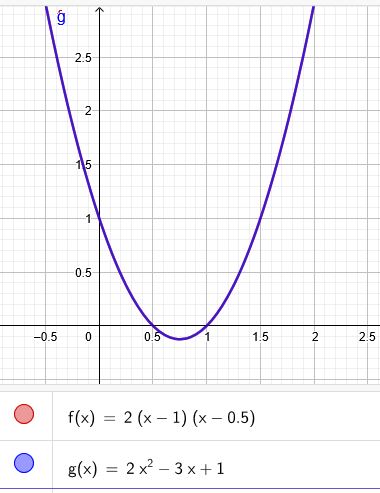
\(f(x)=2 \cdot (x-1)(x-0,5) \)
\(g(x)=2x^2-3x+1 \)
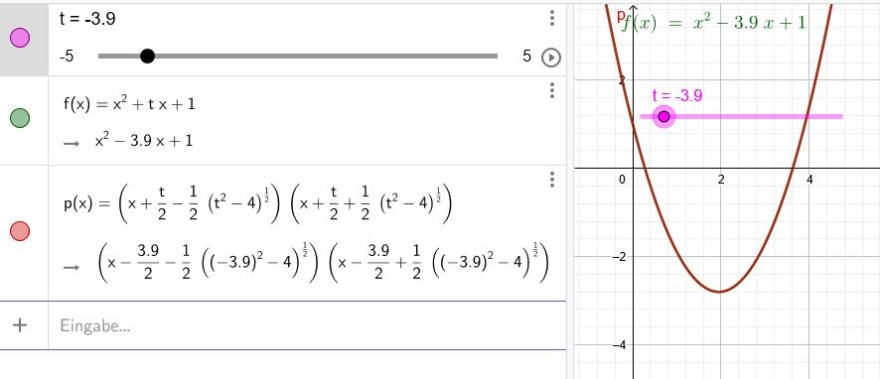
d) \(x^2+tx+1=0\)
Lösungen:
\(x^2+tx=-1\) quadratische Ergänzung:
\(x^2+tx+(\frac{t}{2})^{2}=-1+(\frac{t}{2})^{2}\) Binom:
\((x+\frac{t}{2})^2=-1+\frac{t^2}{4}=\frac{t^2-4}{4} |±\sqrt{~~}\)
1.)
\(x+\frac{t}{2}=\frac{1}{2}\sqrt{t^2-4} \)
\(x_1=-\frac{t}{2}+\frac{1}{2}\sqrt{t^2-4} \)
2.)
\(x+\frac{t}{2}=-\frac{1}{2}\sqrt{t^2-4} \)
\(x_2=-\frac{t}{2}-\frac{1}{2}\sqrt{t^2-4} \)
Zerlegung in Linearfaktoren:
\(x^2+tx+1=[x-(-\frac{t}{2}+\frac{1}{2}\sqrt{t^2-4})][(x-(-\frac{t}{2}-\frac{1}{2}\sqrt{t^2-4})]\\=[x+\frac{t}{2}-\frac{1}{2}\sqrt{t^2-4}][x+\frac{t}{2}+\frac{1}{2}\sqrt{t^2-4}]\)