Vom Duplikat:
Titel: Masse eines Zylinders; inhomogene Masseverteilung
Stichworte: zylinder,masse,integral
es geht um folgende Aufgabe 
Da Dichte ja mit steigender Höhe LINEAR abnimmt, habe ich mir überlegt, ob ich das ganze nicht recht simpel lösen kann indem ich den Mittelwert der zwei "Dichten" einfach mit dem Volumen multiplizieren kann, um an das Gewicht zu kommen.
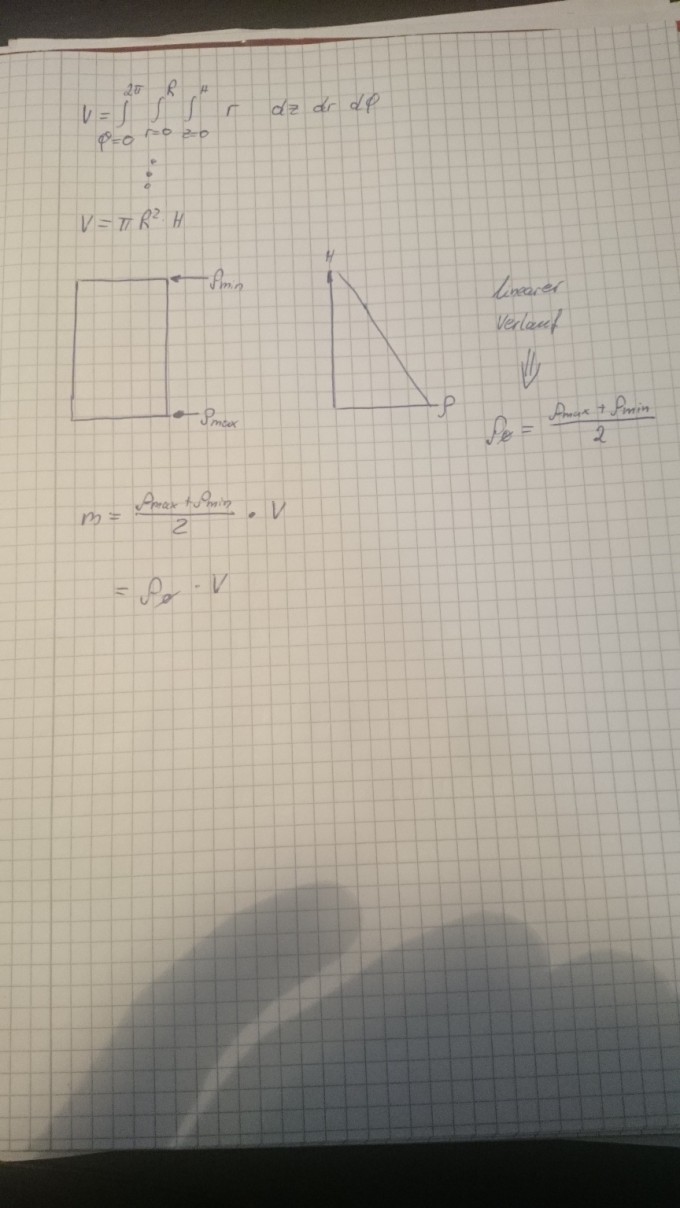
Nur bin ich mir bei diesem Vorgehen überhaupt nicht sicher. Kann mich jemand eines besseren belehren?