Komplexe Zahlen, z^5=-30. Woher das π und was bewirkt das Minus?

Question

z⁵=-30
(re^iφ)⁵=-30=30*[cos(π)+isin(π)]

Fragen:
1.) Woher weiß man, dass es π sein muss?
Was müsste man in den Taschenrechenr genau eingeben?
2.) Was sagt dieses Vorzeichen - aus? Was wäre wenn es + wäre?

Comments

1.) Woher weiß man, dass es π sein muss? 
Was müsste man in den Taschenrechenr genau eingeben? 

π ist ein Winkel im Bogenmass und entspricht 180°. Ich rate ab für jede Aufgabe den Taschenrechner umzustellen. Damit vermeidest du einen der häufigsten "Flüchtigkeitsfehler". 

2.) Was sagt dieses Vorzeichen - aus? Was wäre wenn es + wäre? 

Zeichne deine komplexen Zahlen in der komplexen Zahlenebene (Gaußschen Zahlenebene) ein. Vgl. Unterlagen oder https://de.wikipedia.org/wiki/Gau%C3%9Fsche_Zahlenebene und https://de.wikipedia.org/wiki/Komplexe_Zahl#Komplexe_Zahlenebene

Dann gibt es keine Frage zum Argument (Winkel) von -30 mehr. Man misst im Gegenuhrzeigersinn und beginnt mit der Messung bei der +Richtung der reellen Achse. 

Answer 1

Hallo Probe,

z⁵  = - 30 

( r·e^i·φ )⁵  = - 30  = 30 · [ cos(π) + i · sin(π) ]    ( =  r · [ cos(φ₂) + i * sin(φ₂) ] )  

Ich könnte mir vorstellen, dass dein Problem darin besteht, dass du den Winkel  φ ≠ π in der Eulerdarstellung der Lösungen  z  der Gleichung  (vgl. unten #)  mit dem Winkel φ₂ = π verwechselst

Bei  φ₂  geht es hier nur um das Argument ( = Winkel φ₂ )  der komplexen Zahl - 30.  

Deren  Pfeil im untenstehenden Bild zeigt nach links  auf die komplexe Zahl  -30                  [ = Punkt (-30|0) auf der reellen Achse ] .

Sie hat deshalb den Winkel φ₂ = 180°, der im Bogenmaß den Wert π hat.                                 Der Betrag (Länge des Pfeils) ist natürlich 30.

 

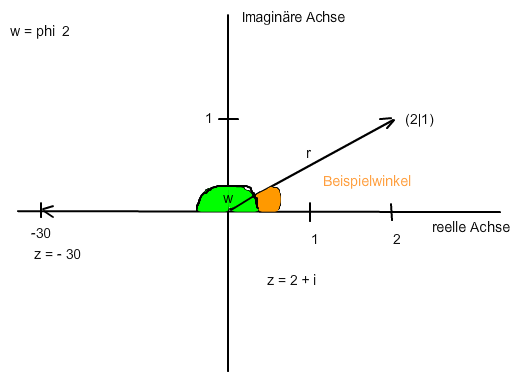
Für die komplexe Zahl 30 rechts auf der reellen Achse wäre der Winkel natürlich 0°.

(#)  

Eine allgemeine Beschreibung für die Berechnung der 5 komplexen Lösungen der Gleichung  z⁵ = - 30 selbst

findest du ggf. bei einer meiner früheren Antworten:

https://www.mathelounge.de/370331/wurzeln-bestimmen-sie-alle-komplexen-losungen-der-gleichung

Bzgl. der 5 Kontrolllösungen für deine Gleichung kannst du ja ggf. nachfragen.

Gruß Wolfgang

Answer 2

-30 : Der zugehörige Pfeil von 0 nach -30 geht in

Richtung der neg. x-Achse, hat also mit der pos.

x-Achse einen Winkel von 180° bzw. im Bogenmaß pi.

Bei + wäre es 0° bzw. Bogenmaß 0.

Answer 3

die Sin und Cos  -Werte von halbzahligen Vielfachen von Pi sollte man schon kennen. 

Dort steht ja

-1+0*i=COS(φ)+ISIN(φ)

Also COS(φ)=-1 und sin(φ)=0.

Daraus folgt φ=π

Dann kann man sich auch leicht merken, dass e^{iπ}=-1 ist.