Vom Duplikat:
Titel: Beweisen Sie die folgende Verallgemeinerung der Bernoullischen Ungleichung
Stichworte: bernoulli,ungleichungen,produktzeichen,summenzeichen
Beweisen Sie die folgende Verallgemeinerung der Bernoullischen Ungleichung: Sind
für i ∈ {1, . . . , n} reelle Zahlen xi ≥ 0 gegeben, so ist
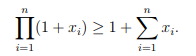
Bemerkung und Zusatzfrage: Sind alle xi
identisch, so erhält man die Bernoullische Ungleichung, die für x ≥ −1 gültig ist. Gilt also die angegebene Ungleichung auch für xi ≥ −1
oder zumindest für xi ∈ [−1, 0] ?