Um die Nullstellen eines Polynoms zu finden, welches dritten Grades oder höher ist, hat man keine so einfachen Formeln wie die abc-Formel oder die pq-Formel zur Verfügung. Dem einen oder anderen mag zwar die Cardanische Formel bekannt sein, doch ist diese oft recht umständlich. Oft reicht es aus, die Nullstelle eines solchen Polynoms als Näherung anzugeben. Dafür sei hier das Newtonverfahren vorgestellt.
Problemstellung: \(x^3+3x^2+2=0\)
Um einen Überblick zu gewinnen ein Schaubild dazu:
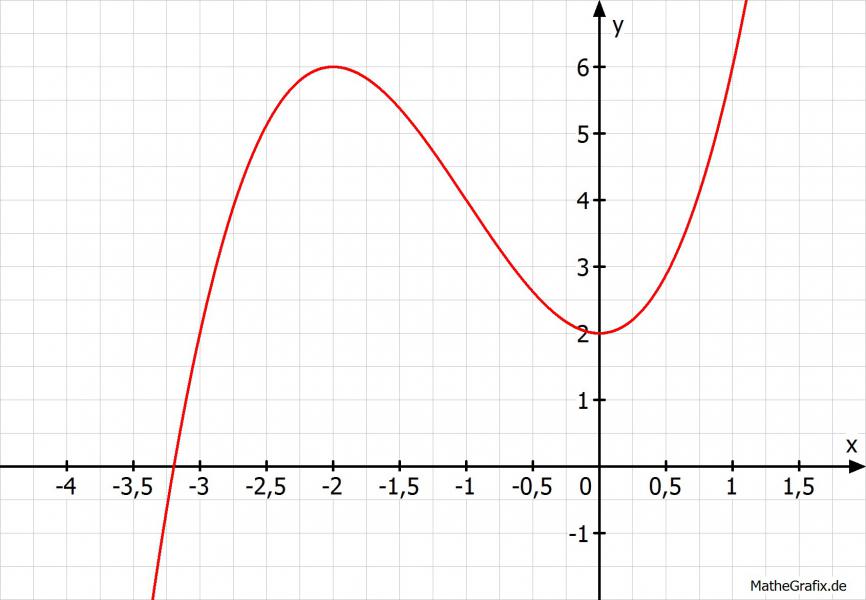
Wir erkennen, dass wir keine "runde" Nullstelle haben und damit sind Verfahren wie Polynomdivision weniger geeignet um diese Nullstelle zu finden.
Hier kommt nun das Newtonverfahren ins Spiel, welches durch folgende Formel beschrieben wird:
$$x_{i+1} = x_i-\frac{f(x_i)}{f'(x_i)}$$
Kann man sich diese Formel merken, hat man den wichtigsten Teil um mit dem Newtonverfahren arbeiten zu können.
Was fehlt ist nun ein geeigneter Startwert um \(x_1\) berechnen zu können. Es darf hierfür ein \(x_0\) fast frei gewählt werden. Es sollte allerdings darauf geachtet werden, dass ein Startwert gewählt wird, der in der Nähe der interessanten Nullstelle zu finden ist. Im Schaubild scheint \(x_0=-3\) als geeignet.
Bevor wir das in die Formel einsetzen, noch etwas Vorarbeit:
Ableitung bestimmen -> \(f'(x) = 3x^2+6x\)
Nun in die Formel damit:
$$x_1 = -3-\frac{f(-3)}{f'(-3)}$$
Nebenrechnung:
$$f(-3) = (-3)^3+3\cdot(-3)^2+2 = 2$$
$$f'(-3) = 3\cdot(-3)^2 + 6\cdot(-3) = 9$$
Wieder in die Formel:
$$x_1 = -3-\frac{2}{9} = -3,22222$$
Wir haben also nun \(x_1\) bestimmt. Aber machen wir weiter.
$$x_2 = x_1-\frac{f(x_1)}{f'(x_1)} = -3,22222 - \frac{f(-3,22222)}{f'(-3,22222)} = -3,19622$$
Führt man das weiterhin fort erhält man:
\(x_1 = \color{red}{-3},22222\)
\(x_2 = \color{red}{-3,19}622\)
\(x_3 = \color{red}{-3,19582}\)
\(x_4 = \color{red}{-3,19582}\)
Das Verfahren wird solange fortgeführt, bis man die gewünschte Genauigkeit hat. Bis sich also die entsprechenden Stellen nicht mehr ändern. Ist man also beispielsweise an einer Genauigkeit von 4 Dezimalstellen interessiert, beobachtet man, ab wann sich die ersten 4 Dezimalstellen nicht mehr ändern. Das ist in unserem Beispiel zum ersten Mal für \(x_3\) und \(x_4\) der Fall, man kann also mit \(x_4\) das Verfahren abbrechen und die Lösung mit N(-3,1958|0) verkünden. Ein Blick auf das Schaubild geworfen bestätigt in etwa das Ergebnis :).
Nahaufnahme:
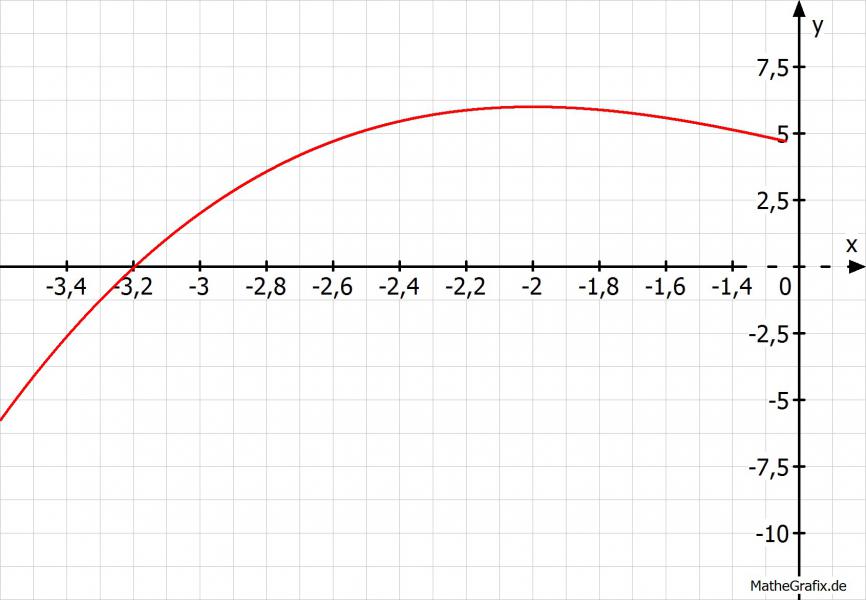
Grüße