Hm, ich vermute mal, du meinst die Folge:
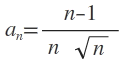
a_n=\frac { n-1 }{ n\quad \sqrt { n } }
Also, für n - > oo, welchen Grenzwert strebt die Folge an?
Allheilmittel: höchste Potenz im Zähler (und Nenner) ausklammern
an = n*(1-1/n)/(n*Wurzel(n)) = (1-1/n)/Wurzel(n)
1 - 1/n für n gegen oo strebt der Term den Wert 1 an. Wurzel(n) für n gegen oo geht gegen oo
1/oo strebt den Wert 0 an. Grenzwert für n gegen oo ist aus meiner Sicht 0.