Hallo Queenie,
f(x) = ax^3 + bx^2 + cx + d
Man erhält ein LGS mit 4 unbekannten, das sich aber recht einfach auf 3 und dann auf 2 Unbekannte reduzieren lässt:
f '(x) = ax^3 + bx^2 + cx + d
f "(x) = 6a·x + 2b
Wendepunkt W(2|1) mit waagrechter Tangente:
f(2) = 8a + 4b + 2c + d = 1
f '(2) = 12·a + 4·b + c = 0
f "(2) = 12a + 2b = 0 ⇔ b = - 6a
Punkt P(3|2)
f(3) = 27·a + 9·b + 3·c + d = 2
b in die drei anderen Gleichungen einsetzen ergibt:
27·a - 3·c - d = -2
16·a - 2·c - d = -1
12·a - c = 0 ⇔ c = 12a
c einsetzen ergibt
9·a + d = 2
8·a + d = 1
Subtrahieren der beiden Gleichungen ergibt a = 1 → d = -7 ; b = - 6 ; c = 12
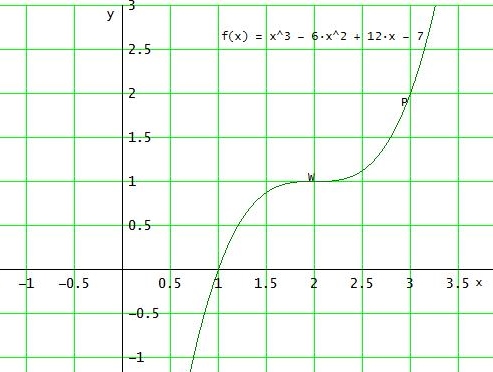
f(x) = x3 - 6x2 + 12 x - 7
Gruß Wolfgang