Vorweg eine Visualisierung des Problems:

(klick das Bild) Ich habe den Zylinder eingezeichnet, für den \(x^2+y^2-2=0\) gilt und die Ebene mit \(x+z-1=0\). Die Schnittmenge ist eine Ellipse im Raum. Auf dieser Ellipse wird der Punkt gesucht, an dem \(f\) lokale Extrema annimmt. Beispielhaft habe ich 4 Punkte \(O\), \(R\), \(U\) und \(L\) darauf markiert. Z.B. ist
$$f\left(O=\begin{pmatrix}-\sqrt{2} & 0 & 1+ \sqrt{2}\end{pmatrix}^T \right) = 2\cdot (- \sqrt{2}) + 4\cdot (1+ \sqrt{2}) = 4 + 2 \sqrt{2}$$ Rechnet man in der Nähe liegende Punkte aus, so kann man vermuten, dass das Maximum zwischen \(O\) und \(L\) liegt. Für die Berechnung der Extrema kannst Du Langrange verwenden (Falls Du nicht weißt, von was ich schreibe, bitte sofort nachfragen). Die vollständige Lagrangefunktion lautet hier
$$\Lambda (x,y,z,\lambda,\mu) = 2x+3y+4z+ \lambda(x^2+y^2-2) + \mu(x+z-1)$$ Ableiten nach \(x\), \(y\) und \(z\) und Nullsetzen ergibt
$$\frac{\text{d}\Lambda}{\text{d}x} = 2 + 2\lambda x + \mu = 0$$ $$\frac{\text{d}\Lambda}{\text{d}y} = 3 + 2\lambda y=0$$ $$\frac{\text{d}\Lambda}{\text{d}z} = 4 + \mu=0$$ aus den letzten beiden folgt
$$\mu = -4; \quad \lambda=-\frac{3}{2y}$$ Einsetzen in die Ableitung nach \(x\) ergibt
$$2 - 2\frac{3}{2y} x -4 = 0 \quad \Rightarrow y=-\frac32x$$ Einsetzen in die erste Nebenbedingung gibt den Wert für \(x\)
$$\frac{9}{4}x^2 + x^2 = 2 \quad \Rightarrow x=\pm 2\sqrt{\frac{2}{13}} \approx \pm 0,7845$$
Daraus folgen dann \(y\) und \(z\) (zweite Nebenbedingung)
$$y= \mp\frac32 \cdot 2\sqrt{\frac{2}{13}} = \mp 3\sqrt{\frac{2}{13}} \approx \mp 1,177; \quad z = 1 \mp 2\sqrt{\frac{2}{13}} \approx 1 \mp 0,7845$$ Ich habe die beiden gefunden Koordinaten eingezeichnet und zusätzlich zwei Ebenen, die jeweils die Menge aller Punkte darstellen, bei denen die Funktion \(f\) einen konstanten Wert hat.
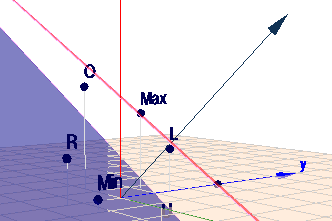
(klick das Bild) Die rote Ebene geht durch das den Punkt \(\text{Max}\) und hat dessen Potential (Wert für \(f\)) und die blaue durch den Punkt \(\text{Min}\). Der Vektor zeigt in Richtung des stärksten Anstiegs von \(f\). Die beiden Ebenen müssen demnach senkrecht zu diesem Vektor liegen. Zwischen ihnen liegen alle anderen Punkte der Ellipse (nicht eingezeichnet). Folglich liegt das Maximum bei
$$(xyz)_{\max} = \begin{pmatrix} -2\sqrt{\frac{2}{13}} & 3\sqrt{\frac{2}{13}}& 1 + 2\sqrt{\frac{2}{13}}\end{pmatrix}$$
und das Minimum bei
$$(xyz)_{\min} = \begin{pmatrix} 2\sqrt{\frac{2}{13}} & -3\sqrt{\frac{2}{13}}& 1 - 2\sqrt{\frac{2}{13}}\end{pmatrix}$$ Gruß Werner