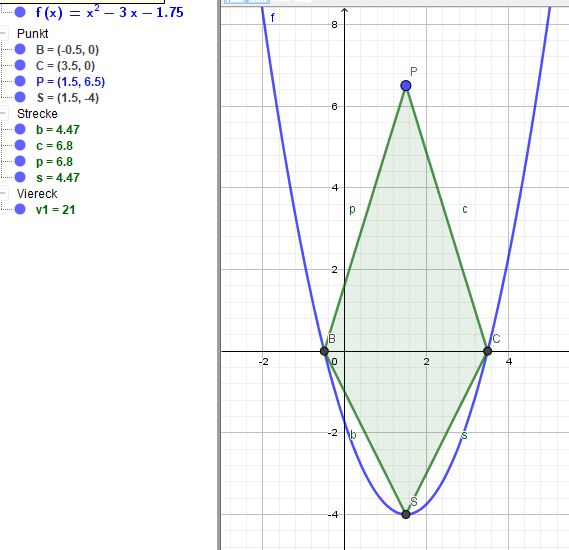
$$ f(x)=x^2-3x-1,75 $$
Um die Parabel zu zeichnen, kannst du den Scheitelpunkt mittels quadratischer Ergänzung bestimmen:
$$ f(x)=(x-1,5)^2-4 $$
Scheitelpunkt bei S(1,5|-4)
Die Nullstellen bestimmst du so:
$$ (x-1,5)^2-4=0\\(x-1,5)^2 = 4\\x-1,5 = 2 \\\text{oder} \\ x-1,5 = -2$$
Damit gibt es Nullstellen bei x = -0,5 und x = 3,5
Du kannst aber auch die Ausgangsgleichung verwenden und mit der pq-Formel arbeiten.
Bei Fragen bitte melden.
Gruß, Silvia