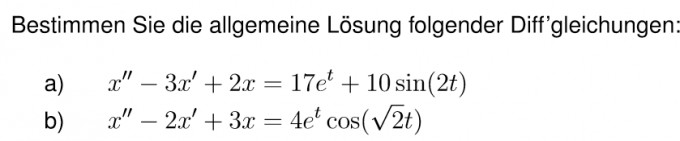Ich weiß, dass man bei der Lösung linearer DGL 2. Ordnung zuerst die homogene Lösung bestimmt und dann die inhomogene.
Die homogene Lösung zu bestimmen habe ich bei a) hinbekommen & bei b nicht (da die Nullstellen komplexe Zahlen sind...)
Wie komme ich bei a) auf die inhomogene Lösung?
Und wie komme ich bei b) auf homogene & inhomogene Lösung?
Würde mich über Antworten freuen
LG