Hallo
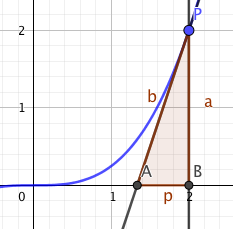
rotiere die Funktion bis x=2 um die x-Achse, dann subtrahiere den Kegel der durch Rotation der farbigen Dreiecks entsteht, indem du a) einfach das Volumen des Kegels ausrechnest, oder das Geradenstück rotieren lässt. oder rotiere die funktion f(x)-t(x). wie man Rotationsvolumen ausrechnet solltest du wissen, oder nachsehen.
Gruß