Korrektur einer Aufgabe ( Integralrechnung)

Question

Ich hoffe jemand kann mir sagen ob der Weg wie ich ihn gewaehlt habe richtig ist und ob es vielleicht einen besseren oder schnelleren Weg gibt. Ich weiß es ist etwas viel aber ich hoffe ich konnte es uebersichtlich und versteandlich zu Blatt bringen un dass die folgenden Information euch vor Arbeit schuetzt !

Der Part mit den linearen Funktion musste ich leider anhand der Grafik ablesen! Ich habe kein Weg gefunden diese mathematisch nur durchs Rechnen zu bekommen

.

Fisch

Flosse

Maul

Fuer jeden Tipp Hinweis auf Fehler oder sonstiges wuerde ich mich freuen.

Oliver

Answer 1

Das sieht bei mir etwas knapper aus

d(x) = (1/36·x^3 - 1/2·x^2 + 9/4·x + 3) - (- 1/54·x^3 + 1/3·x^2 - 3/2·x + 2) = 5/108·x^3 - 5/6·x^2 + 15/4·x + 1

D(x) = 5/432·x^4 - 5/18·x^3 + 15/8·x^2 + x

D(12) - D(0) = 42 FE

A = 42 - 1/2·1·1 - 1/2·6·0.5 = 40 FE = 10 cm² --> 2 g
A = 42 - 1/2·1·1 - 1/2·6·0.5 - pi·0.5^2 = 39.21 FE = 9.804 cm² --> 1.961 g

Comments

Der Part mit den linearen Funktion musste ich leider anhand der Grafik ablesen! Ich habe kein Weg gefunden diese mathematisch nur durchs Rechnen zu bekommen

Die Funktionen selber brauchst du nicht ermitteln. Oder wolltest du die Fläche von Dreiecken mittels Integralrechnung machen.

Dann am besten noch das Auge aus 2 Funktionsgraphen darstellen.

---

Haben in dem Sinne das gleiche Ergebnis raus !

1,875+10.125 sind nicht 11 oder sondern 12 !

Also ziehe ich 1FE ab von 41FE( Mein Ergebnis zuvor)

Und bei der Berechnung der Kosten habe ich nicht die Kosten des Fisches ausgerechnet sondern die Kosten für das Holzbrett 6mal12.

Mit dem Dreisatz und die Berechnung der Kosten von 10cm² bekomme ich das selbe Ergebnis.

Aber eine Frage ist nun hinzugekommen nach deiner Antwort ( Danke nebenbei dafür). Es hat mich gewundert dass man die Funktionen gleichsetzten konnte. Ich dachte das funktioniert nur wenn eine Fläche eingeschlossen ist von 2 Graphen.

Kann ich immer 2 funktionen gleichsetzen und die Fläche immer berechnen egal in welchem Interval ? Wenn ich mir so die " neue " funktion angucke ist es schwer nachzuvollziehen wie dort die gleiche Fläche herauskommen kann wie bei mir. Ich seh ja selber anhand des Integralls das es richtig ist aber optisch ?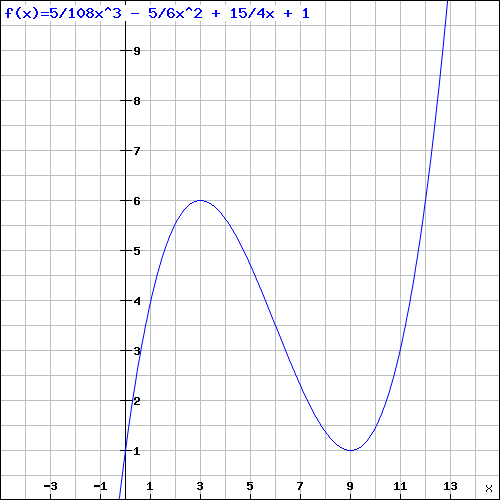

Schwer nachzuvollziehen.

Und ich habe die Funktion mit hilfe von Integralrechnung gemacht. Da es um Integralrechnung geht zurzeit bei uns heatte ich gedacht dass der Lehrer dies auch so sehen will. War ja auch zum Glück richtig so wie ich es gemacht habe :).

Aber werde auf jeden Fall deinen Weg erwaehnen da dieser weitaus schneller geht und die moeglichkeiten Fehler zu machen um einiges geringer ist.

---

Bin extrem anfaellig für Fluechtigkeitsfehler. Hat mich schon oft 2 Noten gekostet und unser Lehrer ist beim korrigieren sehr streng

---

Achja und bezueglich des Auges . Wie soll ich einen Kreis bilden koenn mit zwei funktionen ?

---

Wie soll ich einen Kreis bilden koenn mit zwei funktionen ?

Das brauchst du nicht. Du brauchst auch nicht die linearen Funktionen bilden. Man kann annehmen, dass ihr Dreiecke und Kreise auch ohne die Integralrechnung berechnn dürft.

Aber eine Frage ist nun hinzugekommen nach deiner Antwort ( Danke nebenbei dafür). Es hat mich gewundert dass man die Funktionen gleichsetzten konnte. Ich dachte das funktioniert nur wenn eine Fläche eingeschlossen ist von 2 Graphen.

Ich setzte nicht die Funktionenen gleich sondern bilde die Differenzfunktion. Letzteres darf man immer machen, wenn es um die Fläche zwischen zwei Graphen geht, egal in welchen Intervallen.

Answer 2

Hier erst einmal die Grundskizze

Die Differenzfunktion ist
d = g minus f ( rot minus blau )

Von dieser Funktion wird die Stammfunktion gebildet
S ( x ) = 5/108 * x^4 / 4 - 5/6 * x^3 / 3 + 15/4 * x^2 / 2 + x

Die Integrationsgrenzen müssen nicht unbedingt die
Schnittstellen der beiden Funktionen sein. Die Integrations-
grenzen können auch willkürlich gewählt werden.

Dann wird die Fläche zwischen x = 0 und x = 12 berechnen
[ S ( x ) ] zwischen 0 und 12

A = 42 cm^2

Falls du Fragen hast oder wenn es mit den Aussparungen
weiter gehen soll dann wieder melden.

Comments

Wie wuerde es denn bei folgenden Aufgaben aussehen ? Z.b Aufgabe 5f).

Kann ich mit einer Rechnung alle 3 Flächen errechnen ?

Ich heatte jetzt halt wieder 3 Integrale errechnet. Jeweil von Schnittpunkt zu Schnittpunkt.

Wobei ich bei dieser Aufgabe sogar 4 Rechnungen gemacht heatte da ein Teil unter der x-achse liegt und dieser egal ob mit GTR oder mit hilfe von Internetseiten als ein minus Betrag betrachtet wird und nicht addiert sondern abgezogen wird von der Gesamfläche.

---

Für alle gilt : Differenzfunktion bilden
( egal ob f minus g oder g minus f )
Ist der linke oder rechte Rand eine Senkrechte
dann diesen Wert nehmen.
Dazwischen von Schnittpunkt zu Schnittpunkt
integrieren.
Alle Werte absolut setzen | A | und aufsummieren.
Du kannst einmal für alle 6 Aufgaben die
Integrationsintervalle anführen.

---

1.[1;5]

2.[-1;0] [0;4]

3.[-4;-1] [-1;5]

4.[-1;2]

5[-5;-3] [-3;-1]

6.[-4;-2] [-2;2] [2;4]

So ?

---

a.) 1..5
b.) -1..2
c.) -2 ..4
d .) -5..-1
e.) -4..-1 und -1..5
f.) -4..-2
-2..2
2..4

---

Ja bin von links nach rechts gegangen und noch von oben nach unten . Aber sonst stimmt überein

Welche FE würdest du rausbekommen bei der Aufgabe f im Interval [-2;2] ?

---

Hier die Berechnungen

Achte bitte auf die Qualität des eingestellten
Fotos.

---

Entschuldige nicht darauf geachtet !

Aber wegen deinem Ergebnis.

Im Intervall [-2;2] hast du ja 40.533 habe ich auch soweit aber bei der Flächenberechnung des dritten Teils [2;4] sind es eigentlich auch 11,733 FE wo du aber 28.8 raus hast. Man sieht es ja schon am Graphen dass Fläche A1 und A3 gleich sein muessten was sich bei meiner Rechnung auch bestaetigt hat.

Oder liege ich gerade komplett falsch ?

---

11.73 ist richtig.
Ich hatte von minus2...4 eingegeben.
Insgesamt 64.

---

Ok perfekt.

Ich dank dir