Newton-Verfahren: Startwert finden?

Question

Halllooo,

Beim Newton-Verfahren muss immer ein geeingneter Startwert gefunden werden. Wie findet man diesen, ohne sich im Internet durch einen Plotter einen anzeigen zu lassen? Wird das nicht schon wieder ein sinnloses Ratespiel?

Grüße

Answer 1

Dein Beispiel mit x^5+5x²-25/10*x = 0 ist ungünstig, da es bis für Polynome bis Grad 4 eindeutige explizite Lösungsformeln gibt (Grad 2: pq, Grad 3: PQRST, Grad 4: PQRSTUVW):

Das x (für die 1. Nullstelle bei x₀=0) ausklammern ergibt x^4+5x-25/10=0

http://www.lamprechts.de/gerd/php/gleichung-6-grades.php

für x1 mal als Beispiel ausgeschrieben:

x₁ = 1/12(-5^{1/6}6^{2/3}sqrt((2a)^{1/3}-4(15/a)^{1/3})-6^{2/3}sqrt(4*5^{2/3}(3/a)^{1/3}-(10a)^{1/3}+(12*5^{5/6})/sqrt((2a)^{1/3}-4(15/a)^{1/3})))  mit a=(45+sqrt(2505)); sqrt() steht für Wurzel()

Deshalb mal ein Beispiel, wo eine Nullstelle schwer zu finden ist:

x*x-1-exp(-pow(x-7/5,6)-2)/(pow((x-7/5) * 4,10)+19/100)
=x^2 - e^{-(x - 7/5)^6 - 2}/(1048576 (x - 7/5)^10 + 19/100) - 1
Wolfra m A lpha . com erkennt sie zwar, liefert aber (in letzter Zeit) keine Lösung mehr.

http://www3.wolframalpha.com/input/?i=x%5E2+-+e%5E(-(x+-+7%2F5)%5E6+-+2)%2F(1048576+(x+-+7%2F5)%5E10+%2B+19%2F100)+-+1%3D0

Deshalb weiter mit Plotter:
http://www.gerdlamprecht.de/Liniendiagramm_Scientific_plotter.htm

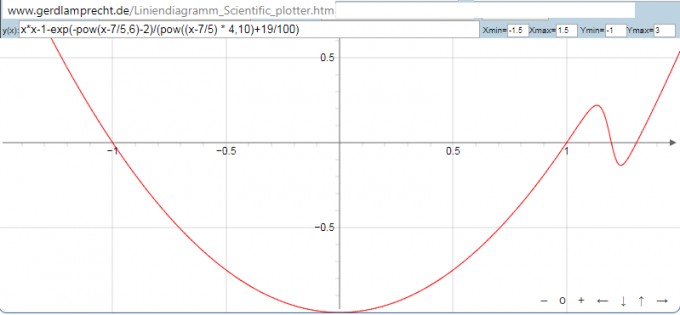
zeigt eine interessante Nullstelle um x=1.2

und Iterationsrechner Beispiel 118:

http://www.gerdlamprecht.de/Roemisch_JAVA.htm

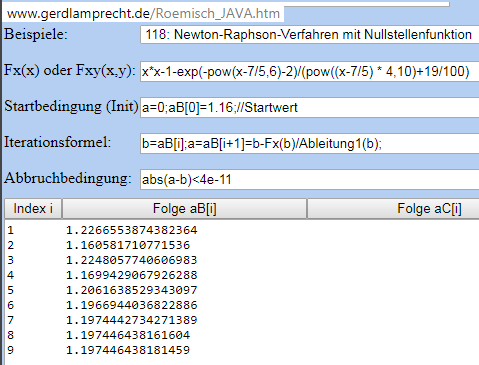
Nur wenn der Startwert im Bereich von 1.16 .... 1.226 liegt, wird diese besondere Nullstelle gefunden.

Man hilft sich aber damit, dass man die Nullstelle bei x4=1.3084833151507...

linksseitig untersucht und somit

x=1.3 -> f(x) kleiner 0

und andere Nullstelle x2=1.00062125927715.. rechtsseitig untersucht:

x=1.1 -> f(x) größer 0

und somit muss es noch ein x3 dazwischen geben. Eine große Wertetabelle braucht man nicht, da die äußeren

Ränder für x1 und x4 leicht und schnell konvergieren.

Comments

Schöne Antwort, aber ich muss gleich nach Frankfurt los. Ich lese mir das, wenn ich zurück bin, ordentlich durch. Ich weiß aber, dass du "Nullstellen-Experte" bist.

---

Darf ich fragen, was du unter "PQRSTUVW" verstehst? Ich löse Polynome vierten Grades mit dem Wiki-Link:

https://de.wikipedia.org/wiki/Polynom_vierten_Grades

---

Ja, im LINK von Wikipedia steht richtig:

"Volle Lösungsformel. Zu kompliziert, um wirklich nützlich zu sein"

Genau diese Formel habe ich analog zur PQRST-Formel hier unter

http://www.lamprechts.de/gerd/Quartische_Gleichung.html

zusammengefasst, bis nur noch die Variablen

P,Q,R,S,T,U,V,W (W₁₂ und W₃₄ ) überblieben und sie "PQRSTUVW" genannt.

{genau wie Leute die quadr. Gl. mal pq oder mal ABC-Formel nennen}

Der Online-Rechner dort ( http://www.lamprechts.de/gerd/php/_gleichung-6-grades.php )

kann komplex rechnen und benötigt keine Fallunterscheidung {wie es noch bei den Cardanischen Formeln nötig war} mehr.

Momentan wird jedoch der Server umgestellt und alle Umlaute und Sonderzeichen zeigen Fragezeichen :-(

Aber ich habe noch einen 2. Server:

http://www.gerdlamprecht.de/gerd/php/_gleichung-6-grades.php

Answer 2

Auch mit einem "ungeeigneten" Startwert führt das Newton-Verfahren schließlich zum Erfolg,aber man weiß nicht, ob sich bei einem anderen Startwert eine andere Nullstelle ergeben hätte. Um nicht in ein sinnentleertes Ratespiel abzugleiten, sollte man eine grobe Vorstellung vom Verlauf des Graphen haben.

Comments

Dass es mit jeglichen Werten geht, das wusste ich nicht. Das mit dem Graphen zeichnen ist zwar eine guter Einwand, aber da ich jegliches Zeichnen hasse, für mich keine gute Option.

Danke für die Antwort

---

Auch mit einem "ungeeigneten" Startwert führt das Newton-Verfahren schließlich zum Erfolg

außer es geht daneben

Dass es mit jeglichen Werten geht, das wusste ich nicht.

Tut es ja auch nicht.

---

Anscheinend schon, man muss nur gucken, wie viele Schritte man braucht...

---

Auch mit einem "ungeeigneten" Startwert führt das Newton-Verfahren schließlich zum Erfolg.

Das ist leider zu optimistisch :-)

---

Nach etwas Nachdenken komme ich zu dem Ergebnis,dass es wohl auch Fälle geben kann, in denen das Newton-Verfahren nicht bei jedem Startwert zum Erfolg führt. Man braucht also umso er eine grobe Vorstellung vom Graphen (hier helfen manchmal die Nullstellen der Ableitungen). Einen Königsweg zu allen Nullstellen aller möglichen Graphen gibt es nicht. Das liegt aber nicht an einer mangelhaften Erforschung,sondern in der Natur der Sache.

---

Man braucht also umso er eine grobe Vorstellung vom Graphen

Was meinst du denn damit ?
Es gibt auf ganz ℝ stetige Funktionen mit Nullstelle 0, für die bei beliebigem Startwert aus dem Intervall (0 ; ε)  (f ist dort selbstverständlich differenzierbar) das Newton Verfahren divergiert.

---

Das liegt aber nicht an einer mangelhaften Erforschung,sondern in der Natur der Sache.

Schade, dass es so viele Grenzen gibt. Vielleicht ist die Mathematik ein falscher Ansatz, um die Welt zu verstehen? Das wäre jetzt aber kaum noch revidierbar.

Answer 3

Hallo Anton,

du kann eine Wertetabelle machen. Wenn du zwei Funktionswerte mit verschiedenen Vorzeichen findest und die Funktion zwischen den zugehörigen x-Werten definiert und stetig ist, hat sie in diesem Intervall mindestens eine Nullstelle und du kannst einen Startwert aus diesem Intervall nehmen.

Für die Frage, ob es weitere Nullstellen gibt, hilft oft die Betrachtung der Ableitungen.

Gruß Wolfgang

Comments

Danke für die weiteren TIpps, bin trotzdem entäuscht von der Mathematik. Es gibt nur Lösungsmethoden (zu Fuß) für Polynome bis zum fünften Grad. Ich habe immer noch eine gewisse Leidenschaft für Polynome, da diese mein Interesse geweckt haben, doch irgendwie wirkt das für mich alles sehr unerforscht.

---

Die Funktion f mit

f(x) = 113 / 216 x⁵ - 259 / 216 x⁴ - 289 / 216 x³ + 527 / 216 x² + 49 / 27 x - 67 / 54

hat zwei Nullstellen im Intervall [1,5 ; 2,5] .
Du kannst ja mal untersuchen, was das Newton-Verfahren bei Startwert 2 macht.

---

Wo hast du denn das schöne Beispiel für die "Eigenwilligkeit" des NV her? :-)

Wegen eines Eingabefehlers geändert:

Lustigerweise findet mein Excel-Programm - wegen des Rundungsfehlers für den genauen Wert 1/3 in der 3. Zeile - tatsächlich eine der Nullstellen im angegebenen Intervall:

---

Wenn man weiß, was man will :

Die ersten drei Zeilen deiner Tabelle hinschreiben und das zugehörige Polynom fünften Grades berechnen - fertig.

Um eine Funktion, deren Existenz in meinem ersten Kommentar behauptet wird, zu finden, muss nur eine einfache Differentialgleichung gelöst werden.

---

Woher weißt du vorher, dass das Polynom aus den 6 Bedingungen aus den ersten 3 Zeilen die "schöne" Wiederholungseigenschaft haben wird?

---

Sehr interessantes Beispiel, danke hj!

---

Ganz einfach :
Ich habe mit den Punkten A bis F angefangen.

 

---

Das ist eine überzeugende Antwort, danke dir :-)

---

Hallo Anton,

damit du nicht zu sehr von der Mathematik enttäuscht bist :-) :

Natürlich kannst du, wenn so etwas passiert - zumindest bei Polynomen - , einfach den Startwert etwas verändern.

Gruß Wolfgang

---

einfach den Startwert etwas verändern.

aber das geht eben leider nicht immer, z.B. bei f mit  f(x) = sign(x) * √ |x|

---

Ich bin trotzdem entäuscht.