Ich stehe vor einem Problem, und zwar geht es um folgendes aus dem Buch Tipler der Seite 1409:
Nicht erschrecken lassen es ist eine Beispiel Aufgabe zur Binomialentwicklung.
Also Berechnen Sie mithilfe von Gleichung \( ( 1 + x ) ^ { n } \approx 1 + x \cdot n \text { für } | x | < 1 \) einen Näherungswert für die Wurzel aus 101.
Problembeschreibung: Die Zahl 101 legt die Zerlegung in das Binom (101 + 1) nahe. Um einen Näherungswert mithilfe der Binomialentwicklung bestimmen zu können, muss man diesen Ausdruck so umfromen, dass wir einen Binom bestehend aus 1 und einem Term kleiner als 1 erhalten.
Lösung:
Schritt 1. Schreiben Sie die Wurzel als (101)^{1/2}; nun können Sie einen Ausdruck der Form (1 + x)^n herleiten, in dem x viel kleiner als 1 ist:
$$ ( 101 ) ^ { \frac { 1 } { 2 } } = ( 100 + 1 ) ^ { \frac { 1 } { 2 } } = 100 ^ { \frac { 1 } { 2 } } ( 1 + 0,01 ) ^ { \frac { 1 } { 2 } } = 10 ( 1 + 0,01 ) ^ { \frac { 1 } { 2 } } $$
Schritt 2. Verwenden Sie Gleichung 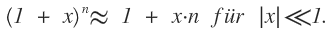 mit n = 1/2 und x = 0,01 und berechnen Sie die Entwicklung von (1 + 0,01)^{1/2}:
mit n = 1/2 und x = 0,01 und berechnen Sie die Entwicklung von (1 + 0,01)^{1/2}:
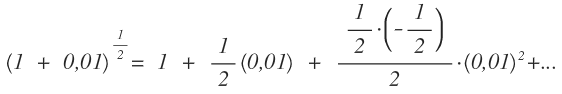
Schritt 3. Wegen |x| << 1 ist zu erwarten, dass der Betrag der Terme von zweiter und noch höherer Ordnung erheblich kleiner ist als der Betrag des Terms erster Ordnung. BestimmenSie einen Näherungsausdruck für das Binom a) nur mit den Termen nullter und erster Ordnung und b) mit den ersten drei Termen:
a) Bei Berücksichtigung nur der Terme nullter und erster Ordnung ergibst sich:
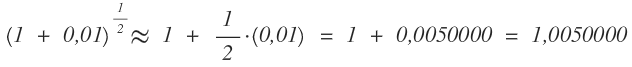
b) Berücksichtigen wir zusätzlich noch den Term zweiter Ordnung, so haben wir:
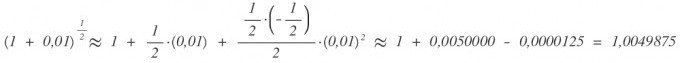
Schritt 4. Setzen Sie diese Ergebnisse in die Gleichung von Schritt 1 ein:
Bei Berücksichtigung nur der Terme nullter und erster Ordnung ergibt sich:
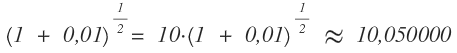
Bei zusätzlicher Berücksichtigung der Terme zweiter Ordnung ergibt sich:
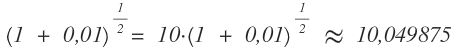
Plausibiltätsprüfung: Es ist zu erwarten, dass unsere Antwort auf 0,001% genau ist. Der Wert von (101)^1/2 beträgt, auf acht gültige Stellen angegeben, 10,049876. Der Unterschied zu 10,050000 beträgt nur 0,000124, der Näherungswert weicht also erst in der vierten signifikanten Stelle ab (1:10000). Zu 10,49875 tritt erst in der siebten signifikanten Stelle eine Differenz auf (1:10000000).
Nun zur Frage:
1. Wie setze ich die Ergebnisse von Schritt 3 in Schritt 4 also in Schritt 1 ein, um auf die 10,050000 zu kommen und 10,049875 ?
2. Bei der Plausibilitätsprüfung verstehe ich nicht wie man auf 0,001 % kommt, auf die acht und vier gültigen Stellen kommt, den Unterschied 0,000124, die Verhältnisse (1:10000) und (1:10000000) und der Näherungswert halt, mit den vier signifikanten Stellen. Hoffe es ist nicht zu lang geworden und freue mich auf jede Unterstützung.
VG :)