Wie berechne ich die Oberfläche eines Dreiecks

Question

Oberfläche eines Dreiecks mit Seiten 3,4,5 cm berechnen. WIe mache ich das?

Comments

Oberflächen haben nur 3 dimensionale Körper.

Answer 1

Hallo Leon,

In diesem Fall ist es sehr einfach, da die drei Seitenlängen $3$, $4$ und $5$ ein sogenanntes pythagoräische Tripel bilden. Es ist $$3^2+ 4^2 = 5^2$$ folglich ist der Winkel gegenüber der Seite mit der Länge $5$  ein rechter Winkel

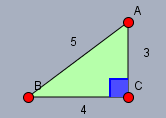
Im rechtwinkligen Dreieck sind die Katheten auch gleichzeitig die Höhen. Folglich ist die Fläche $F$ (nicht Oberfläche) dieses Dreiecks: $$F= \frac12 hg = \frac12 \cdot 3\text{cm} \cdot 4\text{cm} = 6\text{cm}^2$$

Answer 2

Ein Dreieck hat eine Fläche und einen Umfang aber keine Oberfläche.

Comments

https://de.m.wikipedia.org/wiki/Dreiecksfl%C3%A4che

Answer 3

Ein Dreieck mit Seiten 3,4,5 cm ist ein rechtwinkliges Dreieck. Sein Flächeninhalt ist das halbe Produkt der Kathetenlängen: 3·4/2=6