Nochmals: Das hier solltest du erhalten:
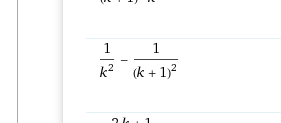
D.h. A = C = 0 und B = 1 und D = -1
Mach dir das Lebe nicht so schwer und erinnere dich an Bruchaddition bzw. Bruchsubtraktion.
(2k+1)/(k^{4}+2k^{3}+k^{2})
= (2k+1)/(k^2(1+2k+k^2)) | quadratisch ergänzen
= (-k^2 + k^2 + 2k + 1)/(k^2(k^2 + 2k + 1)) Bruchaddition
= (-k^2 )/(k^2(k^2 + 2k + 1)) + (k^2 + 2k + 1)/(k^2(k^2 + 2k + 1)) | kürzen
= (-1)/(k^2 + 2k + 1) + 1/k^2
= 1/k^2 - 1/(k+1)^2