Cauchy-Folge |xn-xn+1|<1/q^n mit 0<q<1

Question

Aufgabe:

Es soll bewiesen werden, dass eine Folge (xn) in R mit |xn-xb+1|<1/q^n für 0<q<1 eine Cauchy-Folge ist. No

Problem/Ansatz:

Ich habe mithilfe der geometrischen Summenformel schon bewiesen, dass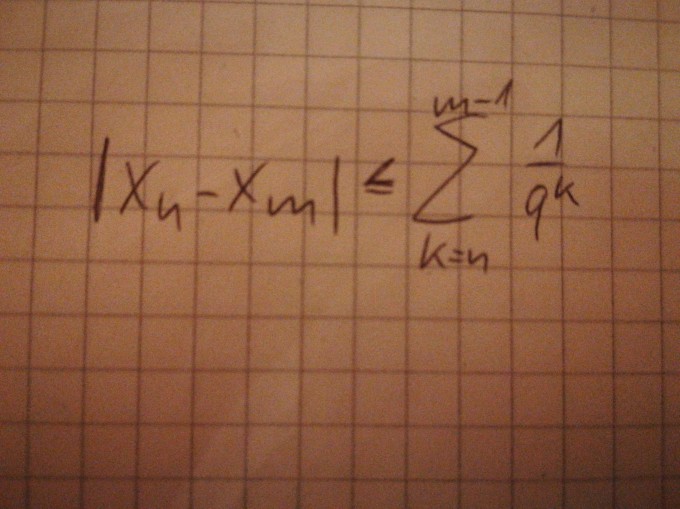

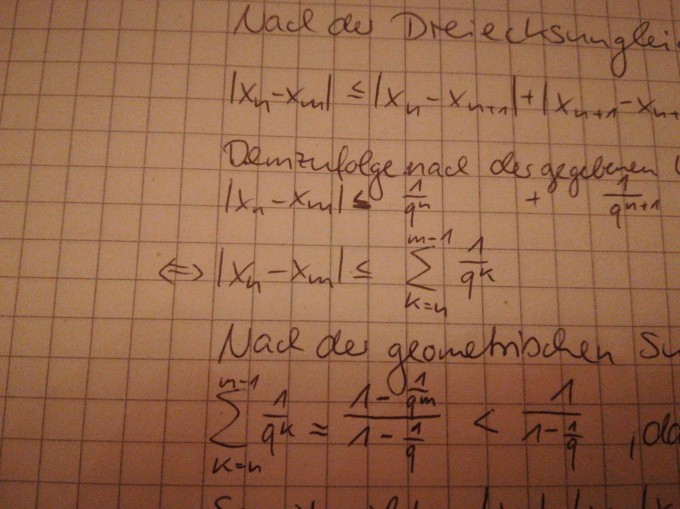
Ignoriert bitte das untere Bild. Das war ein Versehen und ging leider nicht mehr zu löschen.

Diese Formel habe ich dann mithilfe der geometrischen Summenformel umgewandelt zu: ((1/q^n)-(1/q^m))/(1-(1/q). Ab hier komme ich leider einfach nicht mehr weiter. Vielleicht kann mir jemand einen Tipp geben.

Comments

Unser Dozent hat die Aufgabe falsch gestellt. Es muss q^n heißen und nicht 1/q^n. Sonst würden ja die Abstände zwischen zwei Folgegliedern auch immer größer werden, was bei einer Cauchy-Folge nicht der Fall sein kann.

Answer 1

Hallo

hast du nicht die falsche Behauptung? sollte es nicht heissen |x_n-x_n+1|<q^n denn mit 0<q<1 ist 1/q^n doch möglicherweise riesig.

Wenn du diesen Fehler beseitigst kommst du mit $$\sum_{k=n}^{n-m} q^k=\frac{q^{n+1}-q^{m+1}}{1-q}$$ ja auf eine gute Abschätzung wegen q^n ja sehr klein  klammer qⁿ⁺¹ aus.

Mit deiner Ungleichung hast du keine konvergierende Folge!

Gruß lul

Comments

Da frage ich heute nochmal meinen Übungsleiter  ob das vielleicht ein Fehler auf der Übungsserie ist.