Gleichungen mit pq-Formel: Bestimme a ∈ R so, dass die Gleichung genau eine Lösung besitzt

Question

Aufgabe:

Bestimme a ∈ R so, dass die Gleichung genau eine Lösung besitzt

Problem/Ansatz:

was ersetzt man durch p und q und wie rechnet man das aus ?

a) x²+(a+1)x+a=0

b) 2x²+4x=ax+2a

c) x² =a(x-1)

d) x²-a=x+a

Answer 1

Es existiert genau eine reelle Lösung, wenn die Diskriminante gleich null ist.

$D=b^2-4ac$ bei $f(x)=ax^2+bx+c$.

Für a also:

$(a+1)^2-4a=0 \Leftrightarrow a=1$

b: $2x^2+4x=ax+2a \Leftrightarrow 2x^2+(4-a)x-2a=0$

$(4-a)^2-4\cdot 2(-2a)=0 \Leftrightarrow a=-4$

usw.

Comments

Das war aber gerade irgendwie überhaupt nicht die Antwort auf die eigentliche Frage.

---

pq-Formel ist bei diesen Aufgaben nur bedingt hilfreich.

---

Vielen Danke

---

Hallo Larry

Wenn der Fragesteller nur die pq-Formel kennt, wie soll er dann deine Diskriminante verstehen?

---

Der Weg über die PQ-Formel lag möglicherweise recht nahe, was aber nicht heißen muss, dass nicht auch andere Kenntnisse zu quad. Funktionen vorliegen.

Ich kann aber gerne darüberhinaus einen Artikel zur Diskriminante verlinken.

Answer 2

a) x² + (a+1)x + a = 0

p = a + 1 ; q = a

(p/2)² - q = 0 → p²/4 - q = 0 → p² - 4q = 0

(a + 1)² - 4a = 0 --> a = 1

b) 2x² + 4x = ax + 2a

2x² + 4x - ax - 2a = 0

x² + 2x - 0.5ax - a = 0

x² + (2 - 0.5a)x - a = 0

(2 - 0.5a)² - 4(-a) = 0 --> a = -4

c) x² = a(x-1)

x² = ax - a

x² - ax + a = 0

(- a)² - a = 0 --> a = 1 ∨ a = 0

d) x² - a = x + a

x² - x - 2a = 0

(-1)² - (-2a) = 0 --> a = -0.5

Comments

warum in dieser Aufgaben muss  Aufgabe muss man nur die Diskriminante berechnen ?

Dank im Voraus !

---

Die Diskriminante gibt an ob man keine genau eine oder zwei Lösungen bei einer quadratischen Gleichung hat.

Ist die Diskriminante gleich Null, dann hat unsere quadratische Gleichung genau eine Lösung und danach ist in der Aufgabe gefragt.

Answer 3

Aufgabe c)

x²=a(x-1)

x²=ax -a

x²-ax +a=0 ->pq-Formel

x_1.2= a/2 ±√ (a²/4 -a)

->Ausdruck unter der Wurzel muß 0 sein:

a²/4 -a=0

a(a/4 -1)=0 ->Satz vom Nullprodukt

a₁=0

a₂=4

Comments

Vielen Danke

Answer 4

Bestimme $a ∈ ℝ$ so, dass die Gleichung genau eine Lösung besitzt.

Bei einer nach oben oder nach unten geöffneten Parabel muss der Extrempunkt auf der x-Achse liegen, dass die Gleichung nur eine Lösung hat,

c)

$x^2 =a(x-1)$

Schreibung als Funktion:

$f_a(x)=x^2-a(x-1)=x^2-ax+a$  Weg über die Ableitung:
$f'_a(x)=2x-a$
$2x-a=0$
Stelle des Extremwertes $x=0,5a$

→ $f_a(0,5a)=0,25a^2-a\cdot (0,5a)+a=-0,25a^2+a$

$-0,25a^2+a=0$ weil Punkt auf der x-Achse:

$a(1-0,25a)=0$ Satz mit dem Nullprodukt:
$a_1=0$   oder $1-0,25a=0$→$a_2=4$

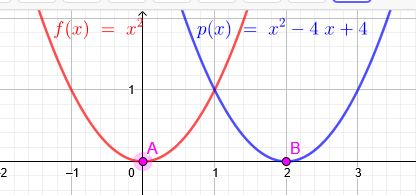
1.Parabel:  $\red{f(x)=x^2}$

2.Parabel:  $\blue {p(x)=x^2-4x+4}=(x-2)^2$