Funktionssynthese, Funktion vierten Grades berührt die Abszissenachse bei x=2

Question

Aufgabe:

Der Graph einer ganzrationalen Funktion vierten Grades berührt die Abszissenachse bei x=2 und hat Wendepunkte im Ursprung und bei x=1,5. Die Steigung im Ursprung beträgt 1

Problem/Ansatz: Ich weiß leider nicht welche Bedingungen ich hier rauslesen soll.

Ich habe einmal f1(2)=0 , f2(1,5)=0 , f1(0)=1    welche fehlen mir noch oder was habe ich hier falsch?

Answer 1

die Bedingungen sollten wie folgt aussehen:

f(2) = 0

f(0) = 0

f''(0) = 0

f'(0) = 1

f''(1.5) = 0

Frag gerne nach, wenn du etwas nicht verstehst.

Comments

Meine Lehrerin meinte wenn dort berührt steht sollte man f(2)=0 und f'(2)=0 schreiben, warum sollte man es denn hier nicht machen? Und warum f(0)=0 ?

Ich verstehe das alles nicht ganz

---

Wendepunkte im Ursprung:

Wenn der Graph im Ursprung O(0/0) einen Wendepunkt hat, dann gilt auch die Bedingung f(0) = 0

---

Deine Lehrerin hat recht. In der Antwort oben wurde die Bedingung f'(2) = 0 vergessen. Die Bedingungen lauten also wie folgt:

f(2) = 0
f'(2) = 0
f(0) = 0
f'(0) = 1
f''(0) = 0
f''(1.5) = 0

Daraus entwickelt man das folgende Gleichungssystem:

32·a + 16·b + 8·c + 4·d + 2·e + f = 0
80·a + 32·b + 12·c + 4·d + e = 0
f = 0
e = 1
2·d = 0
135/2·a + 27·b + 9·c + 2·d = 0

Und daraus ergibt sich dann die Lösung:

f(x) = 0,25·x^4 - 0,75·x^3 + x
f'(x) = x^3 - 2,25·x^2 + 1
f''(x) = 3·x^2 - 4,5·x

Answer 2

Der Graph einer ganzrationalen Funktion vierten Grades berührt die Abszissenachse bei x=2

f(2) = 0

f '(2) = 0 . Berührung der s-Achse impliziert Steigung Null.

 und hat Wendepunkte im Ursprung 

f(0) = 0 , (Geht durch Ursprung)

 f ''(0) = 0

und bei x=1,5.

f ''(1.5) = 0

Die Steigung im Ursprung beträgt 1

f ' (0) = 1 

Answer 3

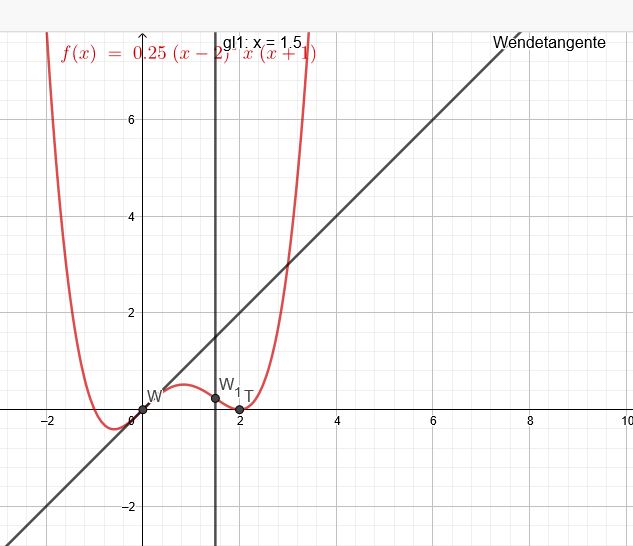
Der Graph einer ganzrationalen Funktion vierten Grades berührt die Abszissenachse bei \(x=2\) und hat Wendepunkte im Ursprung und bei \(x=1,5\). Die Steigung im Ursprung beträgt \(m=1\)

....berührt die Abszissenachse bei \(x=2\): doppelte Nullstelle, weil dort ein Extremum ist.

...und hat Wendepunkt im Ursprung : einfache Nullstelle

Nullstellenform der ganzrationalen Funktion vierten Grades:

\(f(x)=a(x-2)^2x(x-N)\\=a(x^2-4x+4)(x^2-Nx)\\=a(x^4-Nx^3-4x^3+4Nx^2+4x^2-4Nx)\)

Wendepunkt im Ursprung:

\(f'(x)=a(4x^3-3Nx^2-12x^2+8Nx+8x-4N)\)

\(f''(x)=a(12x^2-6Nx-24x+8N+8)\)

\(f''(0)=a(8N+8)=0\)

\(N=-1\)

...Die Steigung im Ursprung beträgt \(m=1\):

\(f'(x)=a(4x^3-9x^2+4)\)

\(f'(0)=4a=1\)

\(a=0,25\)

\(f(x)=0,25(x-2)^2x(x+1)\)

Comments

und hat Wendepunkt im Ursprung : einfache Nullstelle

Ist im Allgemeinen nicht richtig. Es könnte im Falle eines Sattelpunktes (was ebenfalls ein Wendepunkt ist), auch eine dreifache Nullstelle vorliegen.

---

Im Kontext zur Berührung  bei \(x=2\) bleibt nur eine einfache Nullstelle im Ursprung übrig.

---

Es reicht zu schreiben: ‚mindestens eine weitere Nullstelle‘

---

Deswegen schreibe ich ja auch, dass es im Allgemeinen nicht richtig ist.

Man sollte einfach mal beachten, dass Leute, die hier nachlesen, auf die Idee kommen könnten, davon auszugehen, dass immer eine einfache Nullstelle vorliegt, wenn ein Wendepunkt im Ursprung liegt. Solche falschen Schlüsse werden gerne gezogen, wenn man nicht explizit erwähnt, warum das in dem konkret vorliegenden Fall so ist.

Es ist nämlich nicht zu vergessen: Diejenigen, die hier Hilfe suchen haben in der Regel nicht das notwendige Niveau, um genau das alles zu wissen.

---

Außerdem ist die Steigung der Wendetangente im Ursprung 1. Das schließt doch schon einen Terrassenpunkt aus.