Funktionssynthese, Sattelpunkt im Ursprung

Question

was mache ich hier falsch?

Sattelpunkt im Ursprung

Aufgabe:

Problem/Ansatz:

Answer 1

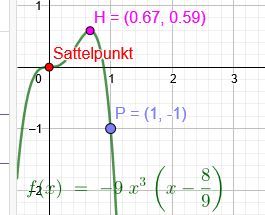
Sattelpunkt im Ursprung bedeutet Dreifachnullstelle:

$f(x)=ax^3(x-N)$

$(1|-1)$:

$f(1)=a(1-N)=-1$                    $a=\frac{1}{N-1}$

$f(x)=\frac{1}{N-1}x^3(x-N)$

Extrempunkt bei $x=\frac{2}{3}$

$f'(x)=\frac{1}{N-1}[3x^2(x-N)+x^3]$

$f'(\frac{2}{3})=\frac{1}{N-1}[\frac{4}{3}\cdot(\frac{2}{3}-N)+\frac{8}{27}]=0$

$N=\frac{8}{9}$   $a=\frac{1}{\frac{8}{9}-1}=-9$

$f(x)=-9x^3(x-\frac{8}{9})$

Answer 2

Wieso gehst du dieser Annahme nach?

Die Funktion $f(x):=-9x^4+8x^3$ erfüllt alle Bedingungen.

Comments

Ich habe die Lösung von meiner Lehrerin bekommen und da steht es sollte f(x)= x⁴ -2x³ heißen

---

Dann frag mal deine Lehrerin, wie sie den Extrempunkt bei x= 2/3 für f(x)= x⁴ - 2x³ ermittelt hat