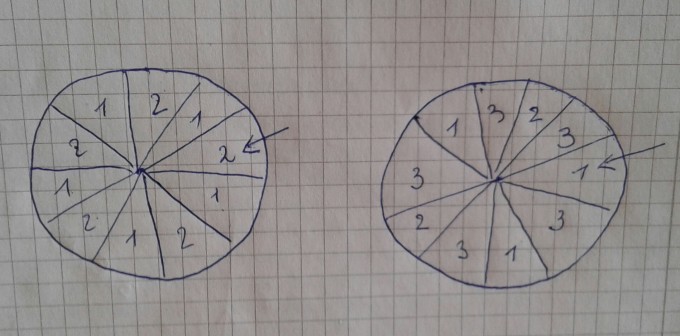
Aufgabe:Zwei Glücksräder sind jeweils in 10 gleiche große Sektoren eingeteilt.
a) Vor dem Drehen der Glücksräder wird folgendes Spiel vereinbart::Zeigen die Pfeile bei beiden Glücksrädern
auf einen Sektor mit der gleichen Zahl, so wird der Betrag in Euro ausgezahlt, den die Zahl angibt. Andernfalls ist der gesetzte Einsatz verloren. Berechnen Sie die Höhe des Einsatzes, damit das Spiel fair ist.
b)Bestimmen Sie die Wahrscheinlichkeit, dass man 3-mal nacheinander gewinnt.
Danke