Regressionsgerade y = ax + b bestimmen

Question

folgende Aufgabe liegt vor:

Bestimmen Sie die Regressionsgerade y = ax + b

Ich wollte nun folgende Werte berechnen:

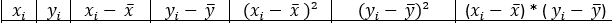
Ich erhalte für

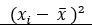  = 3300

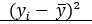  = 12,90821

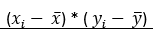  = 651,9

Laut meiner Formelsammlung lassen sich die Werte wie folgt berechnen:

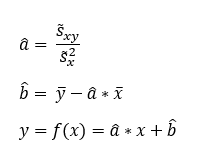
Ich dachte 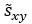 = Kovarianz und  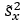= Empirische Varianz

Leider steht in den Lösungen für das zweite

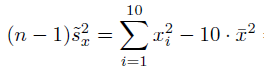
Und für das erste

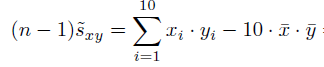
Jetzt meine Frage, was für eine Formel ist das? Wie berechne ich die Regressionsgerade?

Ich würde mich sehr über eine Antwort freuen. Vielen Dank im Voraus und einen schönen Feiertag.

Euer Max

Answer 1

Hallo maax,
geh für den ersten Schritt zur Berechnung genau
wie hier vor.
https://www.mathelounge.de/638460/lineare-regression-durchfuhren-geradenfunktion-bestimmen
und stell deine Werte Summe x,y,x^2 ,xy hier ein.
Dann ist es nicht mehr viel.
mfg Georg

Comments

Guten Morgen georgborn,

erstmal vielen Dank für deine Antwort.

Habe von eine YouTube-Video diese Lösung/Formel gefunden. Ich verwende die Formel Regress. Gerade x.

Dies hat geklappt. Leider bei einer zweiten Aufgabe, stimmt diese Formel nicht mehr. Liegt es an der Formel (also ist die Formel falsch), oder an meiner Wenigkeit :D?

---

Kommentar → Antwort

Answer 2

Für deine 3 oben berechneten Summen (?)  erhalte ich

33000  (statt 3300)

75715,0887 (statt 12,9...)

651,9

RG:  y = 0,01975 · x + 1,21509    [ b = 651,9 / 33000 ≈ 0.01975   ... ]

Nachtrag:

Koeffizienten der Regressionsgeraden  y = b·x + a
$$b=\frac{\sum\limits_{i=1}^{n} (x_i-\overline{x})·(y_i-\overline{y})}{\sum\limits_{i=1}^{n}(x_i-\overline{x})^2}=\frac{ \sum\limits_{i=1}^{n}x_i·y_i-n·\overline{x}·\overline{y} } {\sum\limits_{i=1}^{n}x_i^2-n·\overline{x}^2 }$$$$a=\overline{y}-b·\overline{x}$$Gruß Wolfgang