Tangente einzeichnen rechnerisch bestimmen

Question

Aufgabe:

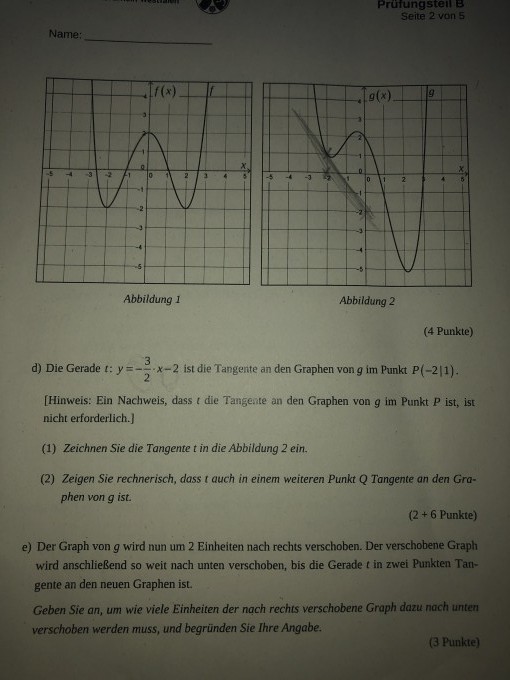
d) Die Gerade \( t : y=-\frac{3}{2} \cdot x-2 \) ist die Tangente an den Graphen von g im Punkt P(-2 |1).

Hinweis: Ein Nachweis, dass t die Tangente an den Graphen von g im Punkt P ist, ist nicht erfojderlich.

1) Zeichnen Sie die rongente t in die Abbildung 2 ein.

2) Zeigen Sie rechnerisch, dass auch in einem weiteren Punkt Q Tangente an den Graphen von g ist.

e) Der Graph von g wird nun um 2 Einheiten nach rechts verschoben. Der verschobene Graph wird anschließend so weit nach unten verschoben, bis die Gerade t in zwei Punkten Tangente an den neuen Graphen ist.

Geben Sie an, um wie viele Einheiten der nach rechts verschobene Graph dazu noch unten verschoben werden muss, und begründen Sie Ihre Angabe.

Wäre so nett wenn mir jemand dabei helfen könnte, dies vor zu rechnen und mir es zu erklären.

Answer 1

d.1) ist ok.

zu d.2):

Comments

Rest vond.2) und e):

---

Dankee❤️ Sehr nett

---

Bitte Texte eingeben. Könntest du das nachreichen? Danke.

Answer 2

Hallo

a)  erster Teil: eine Gerade mit der Steigung -3/2  die durch (-2,1) geht solltest du zeichnen können, da du ka aus der Gleichung weisst, dass sie auch durch (0,-2) geht kannst du sie auch einfach durch die 2 Punkte zeichnen. zweiter Teil g(x) ableiten, feststellen wo die Steigung also g'/x)=-3/2 ist und prüfen, ob der Punkt auf der Geraden liegt.

d) 2 nach rechts verschieben, dann müsste man die Gerade auch 2 nach rechts schieben, statt dessen kann man sie nach unten schieben, da sie die Steigung -3/2 hat kann man sie statt 2 nach rechts auch 3 nach unten schieben, oder du schreibst die nach rechts verschobene Gerade als y= -3/2(x-2)-2=-3/2x+3-2

 damit es wieder die alte wird, muss man also 3 abziehen , also auch den Graphen 3 nach unten schieben

Gruß lul