Stetige Zufallsvariable mit Integral

Question

Aufgabe:

Die Zeitdauer (in Stunden), die ein Computer funktioniert, bevor er abstürzt, ist eine stetige Zufallsvariable mit Dichte

Wie hoch ist die Wahrscheinlichkeit, dass der Computer zwischen 50 und 150 Stunden ohne Absturz
funktioniert? Wie hoch ist die Wahrscheinlichkeit, dass es weniger als 100 Stunden dauert bis zum
Absturz?

Problem:

Wie muss ich verfahren? Gibt es hier eine Art Schritt für Schritt Anleitung? Also was muss ich genau tun? Es würde mich sehr freuen, wenn mir jemand die Schritte sagen könnte, worauf es ankommt und wieso.

Vielen Dank im Voraus!

Euer Max

Comments

Vom Duplikat:

Titel: Dichtefunktion Integral von 0 bis Unendlich und Verteilungsfunktion

Stichworte: verteilungsfunktion,dichtefunktion,stochastik

Aufgabe:

Die Zeitdauer (in Stunden), die ein Computer funktioniert, bevor er abstürzt, ist eine stetige Zufallsvariable mit Dichte.

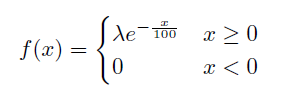
Wie hoch ist die Wahrscheinlichkeit, dass der Computer zwischen 50 und 150 Stunden ohne Absturz
funktioniert? Wie hoch ist die Wahrscheinlichkeit, dass es weniger als 100 Stunden dauert bis zum
Absturz?
Problem/Ansatz:

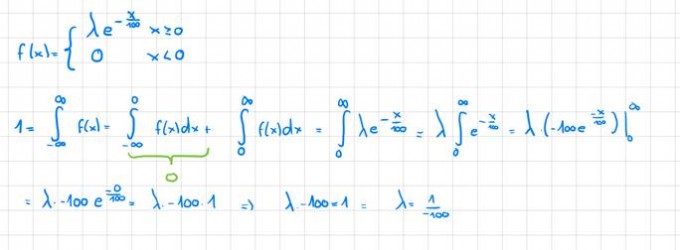
Ich habe bis jetzt, es soweit ausgerechnet. Laut Lösungen erhalte ich 1/100.

Meine Frage ist jetzt, wie berechne ich ein unendlich Integral? Normal wäre es ja (F(B)) - F(A), aber was setzte ich für F(B) ein?

Die Lösung schreib darunter folgendes:

Die Verteilungsfunktion erhält man für x > 0 durch Integrieren der Dichtefunktion

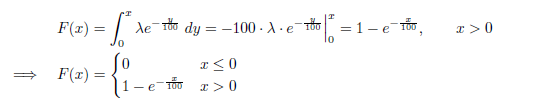
Was sagt mir diese Verteilungsfunktion aus und wie komme ich darauf?

Ich würde mich sehr über eine Antwort freuen, vielen Dank im Voraus!

---

aber was setzte ich für F(B) ein?

Den Grenzwert x gegen unendlich. Siehe uneigentliche Integrale.

---

Was meinst du warum ich dir empfohlen habe dich in die Exponentialfunktionen einzulesen und dann zu sagen was du nicht verstehst.

https://www.mathelounge.de/645146/stetige-zufallsvariable-mit-integral

Aber da kam ja nichts mehr von dir.

Answer 1

Aloha :)

Das uneigentliche Integral kannst du berechnen, indem du eine Hilfsvariable \(h\) einführst und diese im Grenzwert gegen \(\infty\) laufen lässt:$$\int\limits_a^\infty f(x)\,dx=\lim_{h\to\infty}\left(\int\limits_a^hf(x)\,dx\right)$$

Zu der Aufgabe:

Wegen \(f(x)=0\) für \(x<0\) reicht es aus, im Folgenden nur \(x\ge0\) zu betrachten. Was auch sinnvoll ist, da der Computer keine negative Lebensdauer haben kann. Das Integral über die Dichtefunktion im Intervall \([a;b]\) gibt an, mit welcher Wahrscheinlichkeit die Lebensdauer des Rechners in diesem Intervall liegt:$$P([a;b])=\int\limits_a^bf(x)\,dx=\int\limits_a^b\lambda e^{-\frac{x}{100}}\,dx=\left[-100\lambda e^{-\frac{x}{100}}\right]_a^b=100\lambda\left(-e^{-\frac{b}{100}}+e^{-\frac{a}{100}}\right)$$Die Verteilungsfunktion \(F(x)\) gibt an, mit welcher Wahrscheinlichkeit die Lebensdauer des Rechners zwischen dem minimal möglichen Wert, hier also \(0\), und \(x\) liegt:$$F(x)=P([0;x])=100\lambda\left(-e^{-\frac{x}{100}}+e^{-\frac{0}{100}}\right)=100\lambda\left(1-e^{-\frac{x}{100}}\right)$$Daher gilt dann auch:$$P([a;b])=F(b)-F(a)$$Das \(\lambda\) kannst du noch aus der Normierung der Gesamtwahrscheinlichkeit auf \(1\) bestimmen, denn irgendwann im Intervall \([0;\infty]\) muss der Rechner ja kaputt gehen:$$1=F(\infty)=\lim\limits_{x\to\infty}\left(100\lambda\left(1-e^{-\frac{x}{100}}\right)\right)=100\lambda\quad\Rightarrow\quad\lambda=\frac{1}{100}$$Damit lautet dann deine Verteilungsfunktion:$$F(x)=1-e^{-\frac{x}{100}}$$

Comments

Erstmal, vielen Dank für die super Antwort!! Eine Frage, habe ich noch,

Wieso ist λ bei der Verteilungsfunktion = 1 ? :)

---

Die Gesamtwahrscheinlichkeit wird immer auf \(1\) bzw. \(100\%\) normiert. Daher muss die gesamte Fläche unter der Dichtefunktion \(f(x)\) gleich 1 sein. Die Fläche bekommst du durch integrieren, also durch die Verteilungsfunktion \(F(x)\). Sie gibt an, wie groß die Fläche unter der Dichtefunktion im Intervall \([0;x]\) ist. Die gesamte Fläche unter der Dichtefunktion ist also gleich \(F(\infty)\). In der vorletzten Zeile habe ich das ausgenutzt. Die Normierung fordert, dass \(F(\infty)=1\) gelten muss, daraus kann man \(\lambda=\frac{1}{100}\) berechnen.

Answer 2

Das ist eine Exponentialverteilung mit λ = 1/100 = 0.01

https://de.wikipedia.org/wiki/Exponentialverteilung

Also bitte einlesen und dann sagen was du nicht verstehst.