Sekante, Tangente und Passante?!

Question

gegeben:   f(x) = 1/t x² + 2

                   g(x) = 3x + 1

 

Frage: Für welchen Wert der Formvariablen im quadratischen Funktionsterm ist die gegebene Gerade Sekante bzw. Tangente bzw. Passante der Parabel?

mein Vorschlag wäre: f(x) = g(x)

dann die Punkte in die Fomel D=b² - 4ac einsetzen und dann schauen bei D=0 ist es eine  Tangente

D > 0 Sekante und D < 0 Pasante

 

ich bin mir nicht sicher ob das so richtig ist, vielleicht weil ich nicht weis was genau gesucht ist.

Answer 1

Ich berechne Schnittpunkte mit 

f(x) = g(x)
1/t * x^2 + 2 = 3x + 1
1/t * x^2 -3x + 1 = 0
x^2 -3t x + t = 0

Damit es nur einen Schnittpunkt gibt muss die Diskriminante Null sein.

p^2/4 - q = 9/4 t^2 - t = 0
t(9/4 t - 1) = 0

t1 = 0
t2 = 4/9

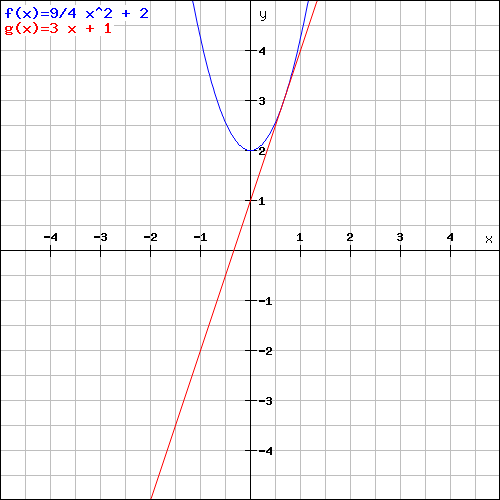
Ich zeichne es mal um zu sehen ob es stimmt:

 f(x) = 9/4 x^2 + 2
g(x) = 3 x + 1