Ein möglicher Weg ist der pow-mod-Algorithmus, wo man ohne große Zwischenergebnisse mit wenigen Schritten den Modulo-Wert von Potenzen bestimmen kann:
24*1 mod 7 =3 ; 24² mod 7=2
3*2 mod 7 =6 ; 2² mod 7=4
6*4 mod 7 =3 : 4² mod 7=2
3*2 mod 7 =6
Der Iterationsrechner unter http://www.gerdlamprecht.de/Roemisch_JAVA.htm
rechnet das online vor:
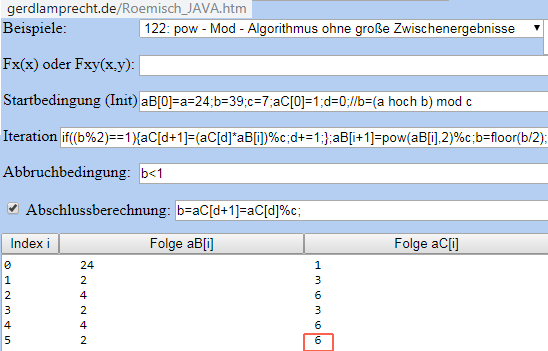
Kleine Offsets beim Argument der Modulo-Funktion vergrößern auch das Ergebnis um diesen Offset:
5 mod 7 =5
(5+1) mod 7 =6
usw.
Wenn 24^39 mod 7 =6 ist, ist der Nachfolger (Offset 1) zunächst 7, aber 7 mod 7 ist 0 -> also kein Rest also durch 7 teilbar!
Mit 53 geht das nicht -> also bleibt 7 der einzige gemeinsame Teiler -> & das Endergebnis.