Wahrscheinlichkeitsraum (Omega, A, P). Bedingte Wahrscheinlichkeiten: Gleichungen zeigen oder widerlegen

Question

hallo. Wie löse ich diese Aufgaben?

Es sei ein Wahrscheinlichkeitsraum ( \( \Omega, \mathcal{A}, P) \) gegeben, sowie die Ereignisse \( A, B \) und \( C \). Widerlegen oder beweisen Sie die folgenden Aussagen zur bedingten Wahrscheinlichkeit:
(a) \( P(A | B)+P(\bar{A} | B)=1, \) falls \( P(B)>0 \)
(b) \( P(A | B)+P(A | \bar{B})=1, \) falls \( P(B)>0 \) und \( P(\bar{B})>0 \)
(c) \( P(A \cup B | C)=P(A | C)+P(B | C)-P(A \cap B | C), \) falls \( P(C)>0 \)

Comments

Hast du https://www.mathelounge.de/677056/beweise-im-diskreten-wahrscheinlichkeitsraum inzwischen verstanden und hier einen Ansatz?

Answer 1

(a) P(A|B)+P(A¯|B)=1, falls P(B)>0, falls P(B)>0

P(A|B)+P(A¯|B)=P(A∩B)/P(B)+P(A¯∩B)/P(B)= [ P(A∩B)+P(A¯∩B) ] /P(B)= [ P(A∩B)+P(B\A) ] /P(B) =P(B)/P(B) = 1

(b) im Sinne Lus:

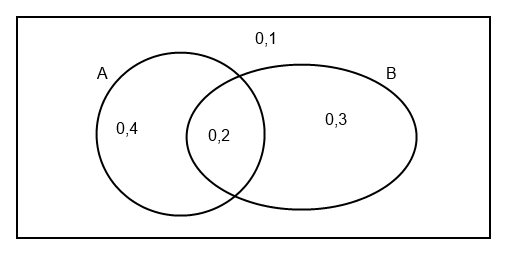
Zeichne zwei sich t.w. überlappende olympische Ringe in einem Rechteck. Schreib an den linken Kreis A, an den rechten B.

Trage die Wahrscheinlichkeiten ein: A\B:0,4   A∩B:0,2       B\A=0,3    außen: 0,1

Dann rechne aus: P(A|B)+P(A|B¯)=...

(c): Schreib die Zeile ab und setze die Definition von "IC" ein. Multipliziere die ganze Gleichung mit P(C).

Dann steht der Additionssatz da im Sonderfall "A"=A∩C, "B"=B∩C

Comments

Können Sie b) und c) auch zeigen?

Mit freundlichen Grüßen

---

"analog" bedeutet eigentlich, dass du im Prinzip a) abschreiben kannst. Versuch das mal.

Aber: Ich vermute, dass man bei b) einfach ein Gegenbeispiel findet. Vgl. https://www.mathelounge.de/230639/diskreter-wahrscheinlichkeitsraum-beweisen-widerlegen

---

Können Sie vielleicht b und c zu Ende führen ?

Mit freundlichen Grüßen

---

Fotografier mal die Zeichnung von b) und stell sie hier ein.

---

Ich habe garkein Zeichnung, ich muss die Aufgabe im Prinzip nach dem Schema wie bei a) lösen.. bloß komm ich nicht drauf wie

---

Mach mal die Zeichnug, sie widerlegt die Aussage.

---

Ich hab leider keinerlei Vorstellung wie die Zeichnung aussehen soll.