Hallo,
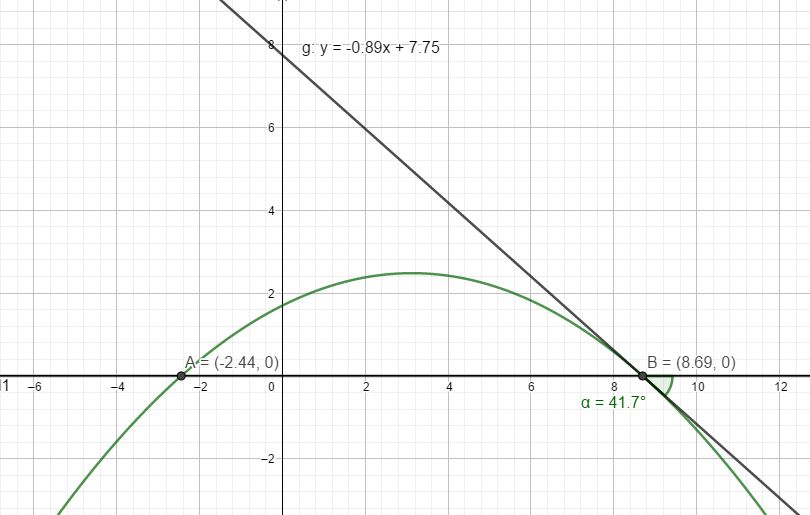
$$f(x)=-0,08x^2+0,5x+1,7\\ f'(x)=-0,16x+0,5\\$$
$$-0,08x^2+0,5y+1,7=0\qquad |:(-0,08)\\ x^2-\frac{25}{4}x-\frac{85}{4}=0\\ x_{1,2}=\frac{25}{8}\pm \sqrt{(\frac{25}{8})^2+\frac{85}{4}}\\ x_1=3,125+5,569=8,694\\x_2=3,125-5,569=-2,444\\$$
$$\tan α=f'(8,694)=-0,89\\ \tan^{-1}(-0,89)=-41,7°$$
Gruß, Silvia