Mit einer Matrix allein also (Mv=w) funktioniert das nicht, da muss zwingend noch eine Translation dazukommen (also eher: Mv + b = w), denn schon wenn man die ersten paar Punkte und deren Bild einzeichnet, kommt man auf einen Widerspruch. Hier eine unprofessionelle Skizze der Speigelung:

Ich rechne das so: (leere Quadrätchen einfach wegdenken; das sollten ja Vektoren sein)

Die Gleichung Nr. 3 zeigt am schnellsten, dass das mit einer Matrix allein nicht geht. Links steht auf jeden Fall 0 und rechts 5.
Man kann aber sofort sagen, was b in Mv + b =w sein muss. (Nämlich b= 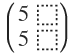
und kann die Matrix in der wie folgt abgeänderten Aufgabe berechnen.

Zum Schluss könnte man sich noch fragen, ob aus x+y = 5 direkt
M =  abgelesen werden könnte.
abgelesen werden könnte.