Definition Wikipedia
eine reelle Funktion ist genau dann gerade, wenn ihr Funktionsgraph achsensymmetrisch zur y-Achse ist, und
f ( x ) = f ( -x )
ungerade, wenn ihr Funktionsgraph punktsymmetrisch zum Koordinatenursprung ist.
f ( x ) = - ( - x )
Test auf gerade in deinem Fall
( x - pi )^2 / 4 = ( -x - pi )^2 / 4
( x - pi )^2 = ( -x - pi ) ^2 | falsch
Test auf ungerade
( x - pi )^2 / 4 = - ( -x - pi )^2 / 4
x^2 - 2pi*x + pi^2 = - ( x^2 - 2pi*x + pi^2 )
x^2 - 2pi*x + pi^2 = - x^2 + 2pi*x - pi^2 | falsch
Die Funktion ist weder gerade noch ungerade.
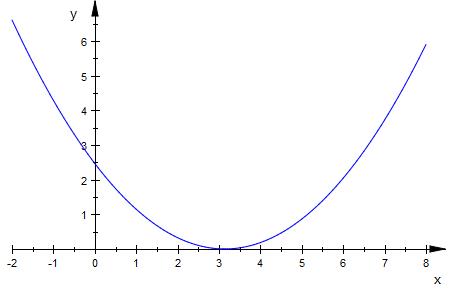
Funktionsgraph