E(x) = 20·x
G(x) = E(x) - K(x) = 20·x - (x^3 - 8·x^2 + 25·x + 14) = - x^3 + 8·x^2 - 5·x - 14
a) Berechne die Gewinnschwelle G, und die Gewinngrenze G,l
G(x) = 0
x = 7 ∨ x = 2 ∨ x = -1
Gewinnschwelle = 2, Gewinngrenze = 7
b) Bestimme das Gewinnmaximum G_l
G'(x) = 0
x = 1/3 ∨ x = 5
Gewinnmaximum bei x = 5
Wie viel € beträgt das maximale Gewinn?
G(5) = 36
Maximaler Gewinn 36
c) Stelle die Funktionsgleichungen für die Stückkosten k(x) und die varibale Stückkosten k_(x) auf!
k(x) = K(x) / x = - x^2 + 8·x - 5 - 14/x
kv(x) = Kv(x) / x = - x^2 + 8·x - 5
d) Erstelle eine Tabelle mit den Stückkosten k(x) und den varibalen Stückkosten für die ME 0: 1: 2:......7!
Eine Tabelle solltest du selber schaffen oder?
e) Berechne das Betriebsminimum U bei wie viel € liegt die kosten Preisuntergrenze?
kv'(u) = 0
8 - 2·u = 0
u = 4
kv(4) = - 4^2 + 8·4 - 5 = 11
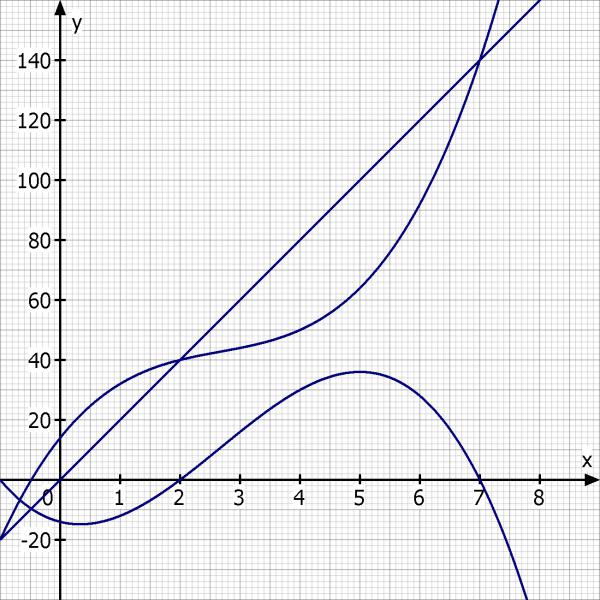
f) Zeichnen Sie in ein gemeinsames Achsenkreuz die Graphen der Gesamtkostenfunktion K(x), der Erlösfunktion E(x) und der Gewinnfunktion G(x). Markiere Gewinnschelle, Gewinngrenze und Gewinnmaximum!