Ich mach mal eine neue Antwort auf, Zwecksübersichtlichkeit:
Den ersten Schnitt kann ich nachvollziehen.
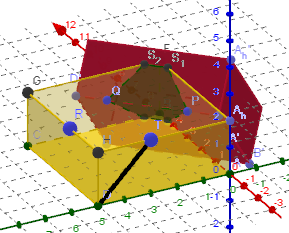
Der Ursprungsquader (gelb) als Abbildung
Translate(Rotate(Rotate(a, 45°, yAxis), -(45°), zAxis), Vector(P' - A))
auf den roten Quader. P(3, 0, 1) wie bei Roland.
T(0, 3, 2), R(2, 5, 2)
Den zweiten Schnitt hab ich nicht verstanden. Wenn man vom Punkt T 45° nach unten in der Länge RT=2sqrt(2) schneidet, dann landet man im Eckpunkt D.
Wie hat man sich den Schnitt vorzustellen? Schnittwinkel?