Question

Aufgabe: Wie kann ich Aufgabe 1c) verstehen? soll ich das Rechteck unter dem Minima ausrechnen oder den Rand der Funktion ab dem Minima bis zum Intervall?

Aufgabe:

Gegeben sei die Funktion $\mathrm{f}$ mit $y=f(x)=\frac{B}{\sqrt{1+\sin (x)}}$

a.) Untersuchen Sie $f$ bzw. ihren Graphen auf Extrempunkte und Polstellen!
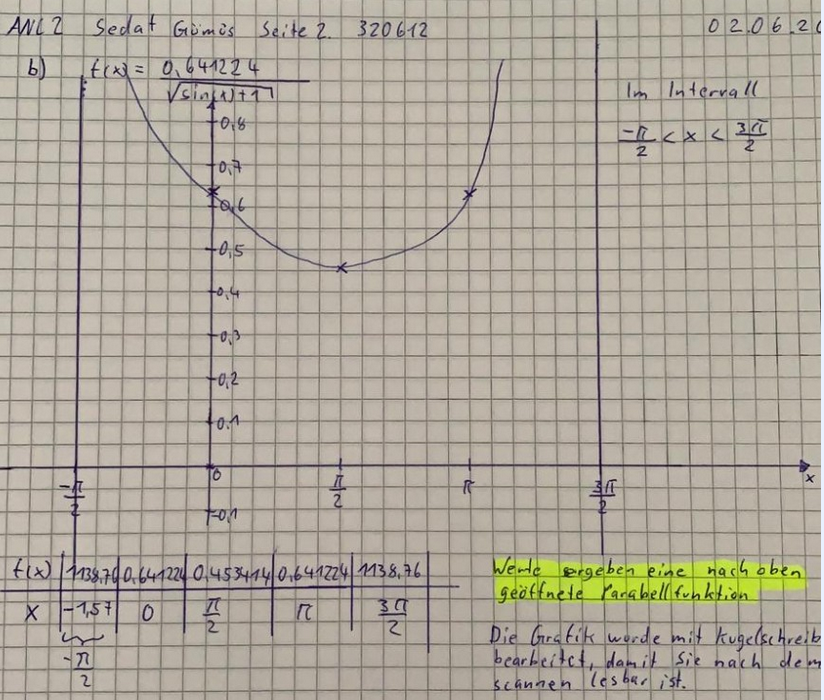
b.) Zeichnen Sie den Graphen von $f$ im Intervall $\frac{-\pi}{2}<x<\frac{3}{2} \pi !$

c.) Berechnen Sie den Zahlenwert des Inhalts der Fläche $A_{T}$, die vom Graphen $f,$ den Koordinatenachsen und der Parallelen zur y-Achse durch den Minimumpunkt begrenzt wird! Der Wert soll 6 Nachkommastellen beinhalten!

Problem/Ansatz:

Aufgaben Verständnis 1c)

Answer 1

Berechne $\int_0^{x_0}f(x)\,\mathrm{d}x$ woebei $x_0$ die x-Koordinate des Minimumpunktes von $f$ ist.

Übrigens, nicht jede Kurve, die nach oben geöffnet ist, ist eine Parabel. In diesem Fall ist es keine.

Comments

Vielen Dank für den Ansatz.

Da sollte eigentlich parabell ähnlich stehen, danke für die berichtigung.