Winkelfunktion. Wie löse ich diese Aufgabe?

Question

Hallo Leute,

Angenommen auf einem DINA4-Blatt Papier wird in der Mitte (Schnittpunkt der Diagonalen) ein Einheitskreis gezeichnet. Dabei entspricht eine Längeneinheit ein Zentimeter. Bis zu welcher Größe des Winkels kann man die zu tan φ ∈[0;90°] gehörende Strecke z auf das Papier zeichnen? Würde mich über Ansätze sehr freuen.

Liebe Grüße

Lisa

Answer 1

TAN(α) = (29.7/2)/1 --> α = 86.14°

Wenn man das Blatt etwas drehen würde, dann könnte die Strecke durchaus noch etwas länger sein.

(21/2)² + (29.7/2)² = a² --> a² = 132309/400

1² + b² = 132309/400 --> b = 18.15963931

TAN(α°) = 18.15963931/1 → α = 86.84°

Answer 2

Hallo Lisa,

ein Bogen DIN A4 hat die Maße 210 x 297 mm. Folgende Zeichnung zeigt den Einheitskreis in der Mitte des Blattes (nicht masstabsgerecht)

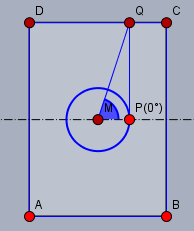
Die Strecke $|PQ|$ ist die halbe Längsseite - also $|PQ| = 29,7 \text{cm} /2$. $|MP|$ ist der Radius des Einheitskreis mit $|MP| = 1 \text{cm}$. Folglich ist der größte Winkel $\varphi_{\max}$ (blau), dessen Tangens noch auf das Papier passt:$$\begin{aligned} \tan \varphi_{\max} &= \frac{|PQ|}{|MP|} = \frac {\frac 12 \cdot 29,7 \text{cm} }{1 \text {cm}} = 14,85 \\ \implies \varphi_{\max} &= \arctan(14,85) \approx 86,15° \end{aligned}$$