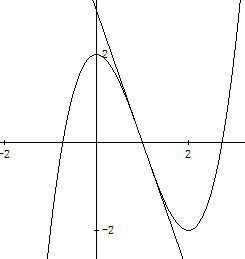Funktion drittes Grades diskutieren

Question

Aufgabe:

Bestimmen Sie die Nullstellen. Die Ableitungen. Die Hoch und Tiefpunkte. Die Wendepunkte. Die Gleichung der Wendetangente und Zeichen Sie den Graphen der Funktion.

Problem/Ansatz:

1) F(x) = x³- 3x²+2

2) F(x ) = x³-x²-4x+4

Answer 1

Hallo

in beiden Fällen die Nullstelle x=1 raten und durch x-1 teilen,  um die 2 weiteren 0 Stellen zu finden dann alles andere wie üblich , oder nimm Assistenzrechner und Plotlux zu Hilfe

Gruß lul

Comments

Gut, dann fang ich mal an. x₁= 1

(x³- 3x²+ 0 x +2) /(x-1) = x² - 2x -2

x³ -  x²                x₂=  1 + \( \sqrt{1+2} \)

 - 2x² + 0 x     x₃= 1 - \( \sqrt{1+2} \)

  - 2x² +  2 x

            - 2 x + 2

              - 2 x + 2

                         0

Answer 2

zu 1)

Die Ableitungen.

F'(x)=3x²-6x

F''(x)=6x-6

F'''(x)=6

Die Hoch und Tiefpunkte.

0=3x²-6x=3x·(x-2), jeder der beiden Faktoren kann 0 sein:

x_E1=0; x_E2=2

F''(0)<0 H(0|2) ist Hochpunkt.

F''(2)>0 T(0|-2) ist Tiefpunkt.

Die Wendepunkte.

6x-6=0 also x_W=1.

F'''(1)≠=; (1|0) ist einziger Wendepunkt.

Die Gleichung der Wendetangente

f '(1)=-3 das ist die Steigung der Wendetangente.

-3=y/(x-1) Punkt-Steigungs-Form der Wendetangente. y=-3x+3 Grundform der Wendetangente.

Zeichen Sie den Graphen

Answer 3

Kurvendiskussion: f(x) = x^3 - 3·x^2 + 2


Funktion & Ableitungen
f(x) = x^3 - 3·x^2 + 2
f'(x) = 3·x^2 - 6·x
f''(x) = 6·x - 6

Nullstellen f(x) = 0
x^3 - 3·x^2 + 2 = 0 → erste Nullstelle bei x = 1 über Wertetabelle
(x^3 - 3·x^2 + 2) / (x - 1) = x^2 - 2·x - 2
x^2 - 2·x - 2 = 0 → x = 1 ± √3 → x = -0.7321 ∨ x = 2.732

Extrempunkte f'(x) = 0
3·x^2 - 6·x = 3·x·(x - 2) = 0 → x = 0 ∨ x = 2
f(0) = 2 → HP(0 | 2)
f(2) = - 2 → TP(2 | - 2)

Wendepunkte f''(x) = 0
6·x - 6 = 0 → x = 1
f(1) = 0 → WP(1 | 0)

Wentetangente
t(x) = f'(1)·(x - 1) + f(1) = 3 - 3·x

Comments

Kurvendiskussion: f(x) = x^3 - x^2 - 4·x + 4


Funktion & Ableitungen
f(x) = x^3 - x^2 - 4·x + 4
f'(x) = 3·x^2 - 2·x - 4
f''(x) = 6·x - 2

Nullstellen f(x) = 0
x^3 - x^2 - 4·x + 4 = 0 → Alle Nullstellen über eine Wertetabelle bei x = 1 ∨ x = ± 2 gefunden.

Extrempunkte f'(x) = 0
3·x^2 - 2·x - 4 = 0 → x = 1/3 ± √13/3 → x = - 0.8685 ∨ x = 1.535
f(1/3 - √13/3) = 70/27 + 26/27·√13 = 6.065 → HP(- 0.8685 | 6.065)
f(1/3 + √13/3) = 70/27 - 26/27·√13 = - 0.8794 → TP(1.535 | - 0.8794)

Wendepunkte f''(x) = 0
6·x - 2 = 0 → x = 1/3 = 0.3333
f(1/3) = 70/27 = 2.593 → WP(0.3333 | 2.593)

Wendetangente
t(x) = f'(1/3)·(x - 1/3) + f(1/3) = 109/27 - 13/3·x

---

und wer rechnet das für Matthieu in seiner nächsten Klausur? Was helfen solche kompletten HA?

lul