Hallo,
Wenn man sich Gedanken darüber macht, wo ein Kreis liegt, der sowohl einen anderen Kreis (blau) als auch eine Gerade (hier die Y-Achse) berührt, kommt man zu folgendem:
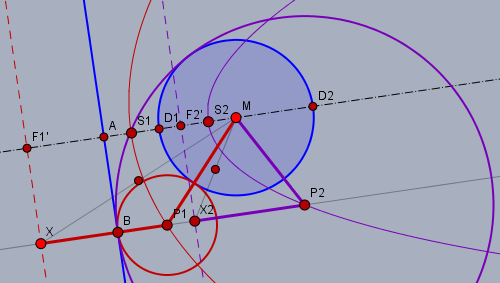
Die Mittelpunkte \(P_1\) und \(P_2\) all dieser Kreise (rot und violett) liegen auf zwei Parabeln, deren Leitgeraden (gestrichelt) um den Radius \(r\) des Ausgangskreises von der Berührgeraden (blau) verschoben sind. Damit die Bedingung der Berührung erfüllt ist, müssen offensichtlich die roten Strecke \(|P_1X|= |P_1M|\) und die violetten Strecken \(|P_2X_2|=|P_2M|\) jeweils gleich lang sein. Und genau das ist die Definition einer Parabel.
Ist die Berührgerade die Y-Achse, so folgen die beiden Parabeln folgender Funktion:$$x-\frac{1}{2}\left(m_{x} \mp r\right)=\frac{1}{2\left(m_{x}\pm r\right)}\left(y-m_{y}\right)^{2} $$wobei \((m_x|\, m_y)\) der Mittelpunkt und \(r\) der Radius des Ausgangskreises ist.
Kombiniert man zwei Kreise, so liegen zwei Parabelpaare mit maximal 8 Schnittpunkten vor, für die diese Bedingung bei beiden Kreisen erfüllt ist. Ich habe mal alle acht möglichen Kreise für diese Aufgabe berechnet:
~draw~ kreis(4|1 6){0c0}{0.3};kreis(-7|-1 9){00c}{0.3};kreis(2.630|-7.521 2.630);kreis(-0.380|4.521 0.380){555};kreis(-4.000|-5.000 4.000);kreis(1.000|5.000 1.000){1};kreis(-0.161|5.096 0.161){c00}{1};kreis(0.587|-4.634 0.587){333};kreis(0.867|-3.066 0.867);kreis(-0.377|5.638 0.377);zoom(12) ~draw~
nur der kleine rote und der gelbe Kreis erfüllen die in der Aufgabe gestellte Bedingung. Sie liegen innerhalb von \(k_1\) (grün) und außerhalb von \(k_2\) (violett). Und die berechnen sich aus folgenden Parabelpaaren:$$\begin{aligned} k_1: &&x-5 &=-\frac{1}{4}\left(y-1\right)^{2}, && r &= -6\\ k_2: && x+8 &=\frac{1}{4}\left(y+1\right)^{2}, && r&= +9\end{aligned}$$ zieht man beide Gleichungen von einander ab, so erhält man eine quadratische Gleichung mit \(y\) als Unbekannte. Hier ist \((x|y) = (1|\,5)\) die gesuchte Lösung für den gelben Kreis und für den kleinen roten Kreis gilt$$\begin{aligned} k_1: && x+1&=\frac{1}{20}\left(y-1\right)^{2}, &&r&= +6\\ k_2: && x-1 &=-\frac{1}{32}\left(y+1\right)^{2}, && r &= -9\end{aligned}$$mit der einen von zwei Lösungen $$\begin{aligned} x &= -\frac 4{169} (5 \sqrt{10} - 9) \approx -0,161 \\ y & = \frac 1{13}(3 + 20 \sqrt{10}) \approx 5,096\end{aligned}$$und den Kreis \(k_1\) habe ich nochmal zum Ausprobieren in Desmos eingegeben:
klickt man auf den Desmos-Schriftzug rechts unten, so öffnet sich der Editor.