Was sind die Nullstellen folgender Funktion?

Question

Aufgabe:

Was sind die Nullstellen folgender Funktion?

f(x) = (5^2x - 6)² - (5^2x - 6) - 12

Comments

Bitte nicht die Aufgabe nachträglich ändern, sodass die Antworten alle falsch werden.

Wenn du Problem bei einer anderen Aufgabe hast, dann stell diese bitte neu ein.

Answer 1

Substituiere in der Gleichung

        0 = (5^2x - 6)² - (5^2x - 6) - 12

mit

(1)        z = 5^2x - 6.

Dann bekommst du die Gleichung

        0 = z² - z - 12

mit Lösungen z = -3 und z = 4. Diese Lösungen setzt du wieder in (1) ein und löst nach x auf.

Comments

Text erkannt:

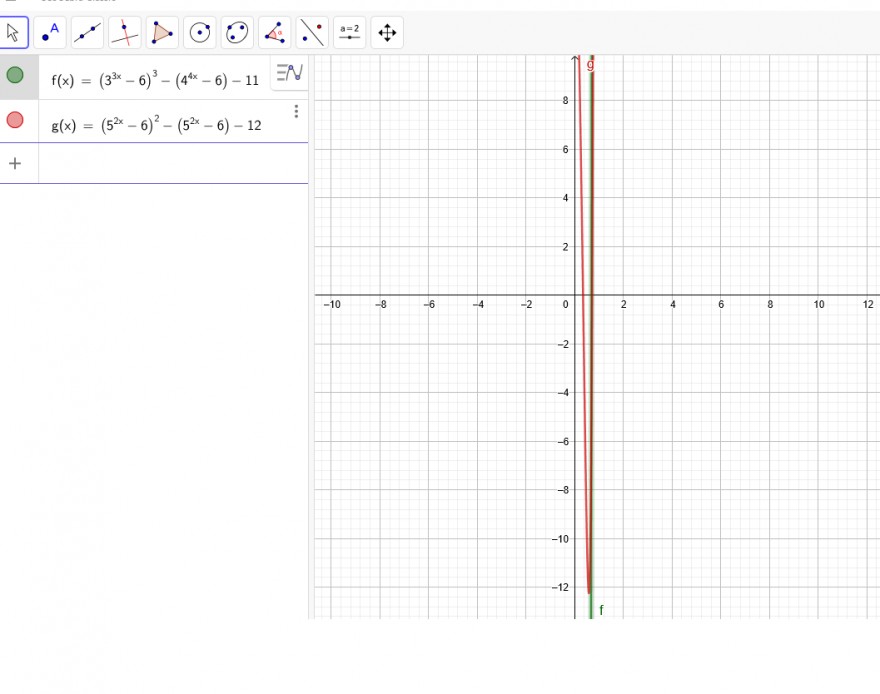
$f(x)=\left(3^{3 x}-6\right)^{3}-\left(4^{4 x}-6\right)-11$
$g(x)=\left(5^{2 x}-6\right)^{2}-\left(5^{2 x}-6\right)-12$

Wie kommst du von f(x) = [3^(3x) - 6]³ - [4^(4x) - 6] - 11

auf    g(x)= [5^(2x) - 6] ² - [5^(2x) - 6] - 12

Im Bild zeigt der grüne Graph eine Nullstelle an und der rote 2 Nullstellen.

mfG

Moliets

---

Dein Kommentar ist irgendwie in die falsche Frage gerutscht.

Answer 2

Substituiere (...) durch z,

quadratische Gleichung lösen

resubstituieren

:-)

Answer 3

z= 5^(2x)-6

z²-z-12 =0

(z-4)(z+3)= 0

z1= 4

z2=-3

5^(2x)-6= 4

5^(2x) = 10

2x*ln5 = ln10

x= (ln10)/2)/ln5

5^(2x)-6 = -3

5^(2x)  = 3

x= (ln3)/2/ln5