Durch welchen Punkt auf der Parabel geht diese Tangente?

Question

Aufgabe:

f(x) =7.5 - 0.5x²

Auf dieser Parabel soll eine Tangente gefunden werden, die durch den Punkt P(8|0) geht. Durch welchen Punkt auf der Parabel geht diese Tangente?

Answer 1

Standardvariante: Ein Punkt auf dem Graphen hat die Koordinaten (x| 7.5 - 0.5x²). Die Gerade durch diesen Punkt und den Punkt (8|0) hat den Anstieg $\frac{7.5 - 0.5x^2 - 0}{x-8}$. Falls der Punkt (x| 7.5 - 0.5x²) der Berührungspunkt mit der Tangente ist, hat die Gerade durch beide Punkte den Anstieg f'(x) Zum Finden der Berührungsstelle löst man also den Ansatz $\frac{7.5 - 0.5x^2 - 0}{x-8} =f'(x)$ nach x auf.

Mögliche Variante bei Quadratischen Funktionen:

Alle Geraden durch den Punkt (8|0) haben die Form y=mx+8.

Gleichsetzen mit $y=7.5 - 0.5x^2$ liefert, falls vorhanden, die Schnittpunkte von Gerade und Parabel. Für bestimmte m gibt es aber nicht zwei Lösungen, sondern nur eine. Dann hat man keine Schnittpunkte, sondern einen Berührungspunkt.

Answer 2

Hallo Karsten,

Die allgemeine Punkt-Steigungsform einer Geraden lautet:$$g: \quad y(x) = m(x- x_0) + y_0$$D.h. die Gerade verläuft durch den Punkt $(x_0|\,y_0)$ und hat die Steigung $m$. Das gilt genauso für eine Tangente. Der Stützpunkt ist der Berührpunkt $B$ auf der Parabel und die Steigung ist die Steigung der Parabel in $B$. Sei die Funktion der Parabel $f(x)$ und liegt der Berührpunkt bei $x=u$ und somit $B$ bei $B(u|\,f(u))$, so lautet die Tangentengleichung$$t: \quad y(x) = f'(u)(x-u) + f(u)$$In Deinem Fall ist $$f(u) = 7,5 - 0,5u^2 \\ f'(u) = -u$$und die konkrete Tangentengleichung in $u$ lautet$$\begin{aligned}y(x) &= -u(x-u) + 7,5-0,5u^2 \\&= 0,5u^2 - ux + 7,5\end{aligned}$$Die Tangente muss durch den Punkt $P(8|\,0)$ verlaufen, also ist$$y(8) = 0$$Einsetzen in die Tangentengleichung gibt:$$\begin{aligned} 0 &= 0,5u^2 -8u + 7,5 &&|\, \cdot 2\\ 0 &= u^2 - 16u + 15 &&|\, \text{pq-Formel}\\ u_{1,2} &= 8 \pm \sqrt{64 - 15} \\ &= 8 \pm 7\\ \implies u_1 &= 1, \quad u_2 = 15 \end{aligned}$$Es gibt also zwei Tangenten durch $P$ an die Parabel. Sie berühren die Parabel in $B_1(1|\,7)$ und $B_2(15|\,-105)$.

Das Bild zur Aufgabe:

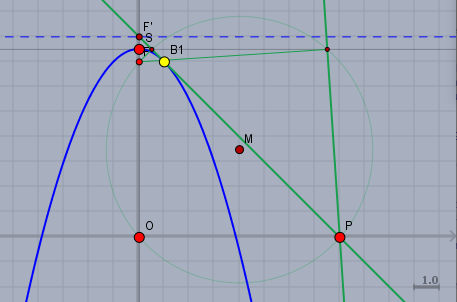
Der zweite Berührpunkt ging nicht auf's Bild.

Gruß Werner

Comments

Habe alles verstanden, vielen vielen Dank!!