könnte mir jemand zeigen wie diese Aufgabe geht? Dankeschön!
Text erkannt:
Ableitung und Integral von Polynomen
Bezeichne \( V_{n}=\mathbb{R}[x]_{n} \) den Vektorraum der reellen Polynome in \( x \) bis zum Grad \( n \). Wir definieren die linearen Abbildungen der Ableitung und des Integrals:
$$ D: V_{5} \rightarrow V_{4}, P \mapsto P^{\prime}, \quad \text { und } \quad I: V_{5} \rightarrow \mathbb{R}, P \mapsto \int \limits_{-1}^{1} P(x) \mathrm{d} x $$
Bestimmen Sie die darstellenden Matrizen von \( D \) und \( I \) in der Standardbasis \( \left(x^{k}\right)_{k=0, \ldots, n} \) von \( V_{n} \) Geben Sie die Kerne von \( D \) und \( I \) an.
Bezeichne \( V_{n}=\mathbb{R}[x]_{n} \) den Vektorraum der reellen Polynome in \( x \) bis zum Grad \( n \). Wir definieren die linearen Abbildungen der Ableitung und des Integrals:
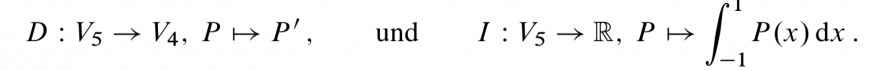
Text erkannt:
\( D: V_{5} \rightarrow V_{4}, P \mapsto P^{\prime}, \quad \) und \( \quad I: V_{5} \rightarrow \mathbb{R}, P \mapsto \int \limits_{-1}^{1} P(x) \mathrm{d} x \)
Bestimmen Sie die darstellenden Matrizen von \( D \) und \( I \) in der Standardbasis \( \left(x^{k}\right)_{k=0, \ldots, n} \) von \( V_{n} \) Geben Sie die Kerne von \( D \) und \( I \) an.